Мономолекулярные реакции и теория активного комплекса

В мономолекулярной реакции переход молекулы в активное состояние схематически можно представить как:

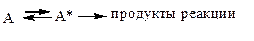
Тогда основное уравнение активного комплекса будет иметь вид:

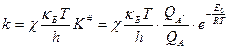
Запишем уравнение k согласно методу активного комплекса и с учетом внутренних колебательных степеней свободы молекулы.

В активном состоянии число степеней свободы колебательного движения 3n – 7, а в исходной молекуле 3n – 6 (где n – число атомов в молекуле).

Статистическая сумма состояния одного колебания:

Полная статистическая сумма состояний колебательного движения равна произведению выражения для отдельных колебаний по всем степеням свободы:

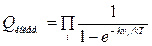
где i — число колебательных степеней свободы.

С учетом этих выражений имеем, что:

Практическое использование уравнения затруднено тем, что в большинстве случаев неизвестны частоты колебаний ν^* в активном комплексе (АК). Поэтому считают, что значения частот колебаний в исходной молекуле ν и в АК ν^* близки (ν = ν^*).

Тогда получают практически применимое выражение для константы скорости:

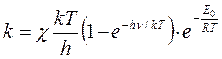
где ν — формально соответствует частоте колебаний в исходной молекуле, отсутствующей в АК;

значение χ близко к 1, поскольку активация в мономолекулярных реакциях является процессом накопления колебательной энергии на внутренних степенях свободы молекулы и не сопровождается переходом на возбужденный электронный уровень, то есть является процессом адиабатическим;

значение предэкспоненциального множителя сек^-1 и имеет хорошую сходимость с экспериментальными величинами.

Отклонения предэкспоненты от величины 10¹³ сек^-1 можно объяснить тем, что в значение предэкспоненты входит энтропия активации согласно методу АК для константы скорости бимолекулярной реакции:

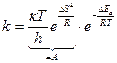
(4)

Опыт по уравнению Аррениуса дает зависимость:

(5)

Согласно уравнению (4) предэкспонента равна cек^-1, но с учетом экспериментальной зависимости предэкспонента имеет приближенное значение

Отсюда можно определить энтропию активации:

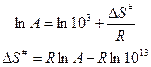
Если в результате расчета получается положительное изменение энтропии, то это указывает на неупорядоченность структуры активного комплекса по сравнению со структурой исходной молекулы, что представляется наиболее логичным.

3. Тримолекулярные реакции в теории столкновений и активного комплекса

Дата добавления: 2014-01-06