Закон сохранения механической энергии материальной точки и

механическом системы. Если на материальную точку или механическую систему действуют только консервативные силы, то в любом поло­жении точки или системы сумма кинетической и потенциальной энергий остается величиной постоянной.

Доказательство:

Для материальной точки на основании теоремы об измене­нии кинетической энергии

.

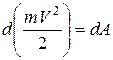С другой стороны, .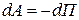

Тогда

.

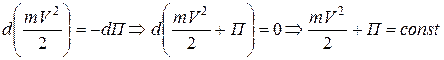Для механической системы аналогично

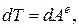a ,

тогда

,

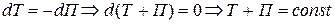где Т+ П — полная механическая энергия системы.

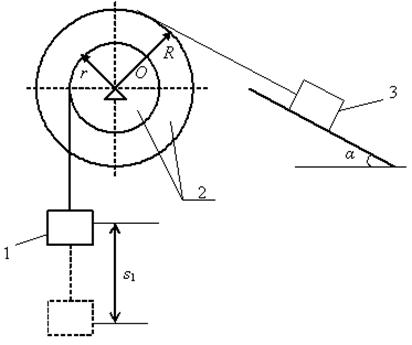
Задача 5. Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывая трение скольжения тела 3, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость и ускорение тела 1 в тот момент, когда пройденный им путь станет равным s (рис. 3.70). В задаче принять:

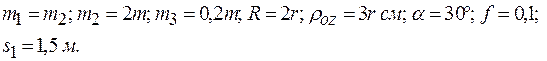
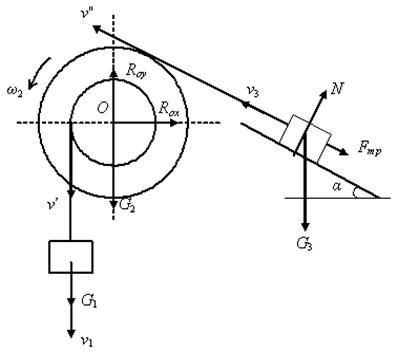
Решение. На механическую систему действуют активные силы , , 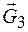. Применяя принцип освобождения от связей системы, покажем реакции шарнирно-неподвижной опоры 2 и шероховатой наклонной поверхности. Направления скоростей тел системы изобразим с учетом того, что тело 1 спускается.

Задачу решим, применяя теорему об изменении кинетической энергии механической системы:

,

где Т и 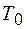– кинетическая энергия системы в начальном и конечном положениях; - алгебраическая сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; - сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями,

.

Так как в начальном положении система покоилась, то . Следовательно,

.

а)

б)

Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1, 2, 3

.

Кинетическая энергия груза 1, движущегося поступательно, равна:

.

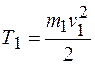Кинетическая энергия блока 2, совершающего вращение вокруг оси Оz, перпендикулярной плоскости чертежа,

.

Кинетическая энергия тела 3 в его поступательном движении

.

Таким образом,

.

Выражение кинетической энергии содержит неизвестные скорости всех тел системы. Начать определение необходимо с 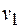. Избавимся от лишних неизвестных, составив уравнения связей.

Уравнения связей это не что иное, как кинематические соотношения между скоростями и перемещениями точек системы. При составлении уравнений связей выразим все неизвестные скорости и перемещения тел системы через скорость и перемещение груза 1.

Скорость любой точки обода малого радиуса 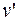равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения r

.

Отсюда выразим угловую скорость тела 2

. (а)

Вращательная скорость любой точки обода блока большого радиуса , с одной стороны, равна произведению угловой скорости блока и радиуса вращения, а с другой – скорости тела 3

.

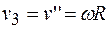Подставив значение угловой скорости, получим:

. (б)

Проинтегрировав при начальных условиях выражения (а) и (б), запишем соотношение перемещений точек системы:

. (в)

Зная основные зависимости скоростей точек системы, вернемся к выражению кинетической энергии и подставим в него уравнения (а) и (б):

.

Момент инерции тела 2 равен:

.

Подставляя значения масс тел и момента инерции тела 2, запишем

.

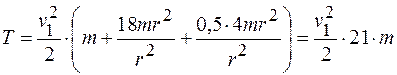Определение суммы работ всех внешних сил системы на заданном перемещении.

.

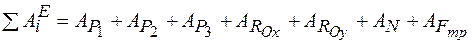Работа силы тяжести тела 1

.

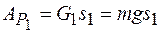Работа сил 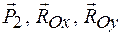равна нулю, так как эти силы приложены к неподвижной точке.

.

Работа силы тяжести тела 3

.

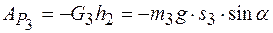Работа нормальной реакции тела 3 равна нулю, так как сила перпендикулярна направлению движения

.

Работа силы трения скольжения

,

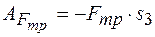так как

,

тогда

.

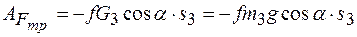Сумма работ внешних сил

.

Подставляя значения масс тел, соотношения перемещений (в) и числовые параметры, запишем:

Теперь согласно теореме об изменении кинетической энергии механической системы приравняем значения Т и

. (г)

Скорость тела 1 получим из выражения (г)

.

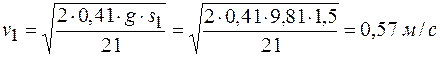Ускорение тела 1 можно определить, продифференцировав по времени равенство (г):

,

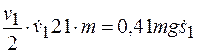где .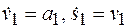

Тогда

.

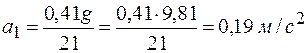Задача 6. Каток для раскатывания асфальта (рис. 62) состо­ит из кузова массой т ₁ = 3∙103 кг и двух одинаковых барабанов. Масса барабана m ₂ = 103 кг, радиус его r = 0,5 м, а радиус инерции — ρ = 0,4 м. Коэффициент трения каче­ния барабанов f_к = 9 см. Определить величину вращающего момента М, передаваемого от двигателя на ведущий бара­бан катка, необходимую для придания кузову ускорения а = 0,2 м / с ².

Рис. 62 Рис. 63

Решение. Поскольку рассматривается мгновенное со­стояние системы, то следует применить теорему об изме­нении кинетической энергии в дифференциальной форме

.

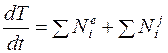Кинетическая энергия системы (поступательно движу­щийся кузов и совершающие плоское движение бараба­ны) имеет вид

,

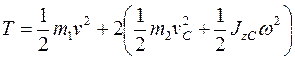где v — скорость кузова, v_С — скорость центра масс бара­бана, ω — его угловая скорость, J_zC = m ₂ ρ ² = 160 кгм ² — момент инерции барабана относительно его оси (проходя­щей через центр масс).

Кинематические связи определяются тем, что каждый барабан поворачивается вокруг своего мгновенного центра скоростей (точки Р), а именно: v_C = ωr; кроме того, v = v_C, т. е. ω = v / r. Тогда кинетическая энергия приводится к виду

,

где 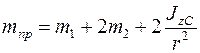= 6280 кг — приведенная к ку­зову масса системы. Производная от кинетической энер­гии по времени равна

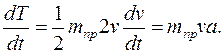
Рассмотрим действующие в системе силы (рис. 63).

Внешние силы. Силы тяжести барабанов G ₂ и кузова G ₁ будут иметь нулевую мощность, поскольку они перпен­дикулярны скоростям точек их приложения. Также нуле­вую мощность будут иметь нормальные реакции R_n и и силы трения F_тр и 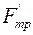, так как равны нулю скорости их точек приложения — мгновенных центров скоростей.

Сопротивление качению учтем, используя вторую мо­дель, т. е. не смещая нормальные реакции, а вводя момен­ты сопротивления качению: и .

Суммарная мощность внешних сил — мощность этих моментов

.

Из условия отсутствия движения центра масс системы вдоль вертикали следует равенство нулю суммы проекций всех сил на вертикальную ось, откуда легко получаем R_n + R '_n = G ₁ + 2 G ₂. Тогда

.

Внутренние силы. Учтем, что за счет работы двигателя на ведущий барабан и на кузов будут действовать одина­ковые по модулю, но противоположно направленные вра­щающие моменты М и М ' (закон равенства действия и противодействия). Заметим, что хотя эти моменты отно­сятся к числу внутренних сил, в данном случае они долж­ны учитываться, поскольку система не является неизме­няемой (имеется взаимное проскальзывание тел системы: кузова и барабанов).

Запишем, учитывая, что кузов не вращается, суммар­ную мощность внутренних сил (моментов)

.

Тогда сумма мощностей всех сил запишется в виде

.

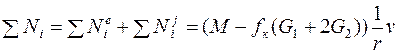Множитель, стоящий в этой формуле перед скоро­стью, — это приведенная сила системы

.

Итак,

.

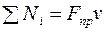Собирая правую и левую части теоремы, получаем т_прav = F_npv, откуда найдем необходимую приведенную силу F_up = m_npa = 1256 Н.

Из выражения для приведенной силы найдем необхо­димую величину вращающего момента М: М = F_npr + + f_к (G ₁ + 2 G ₂) = 5,04 кНм.

Анализируя численные величины слагаемых в послед­ней формуле, можно отметить, что на преодоление сопро­тивления качению в данном случае требуется значительно больший вращающий момент, чем на разгон катка, т. е. придание ему ускоренного движения.

Ответ: М = 5,04 кНм.

Задача 7. Для рассмотренного в предыдущей задаче катка опре­делить скорость его кузова после того, как он прошел расстояние s = 2 м, если к ведущему барабану приложен постоянный вращающий момент М = 4,6 кНм, а началь­ная скорость катка была равна v ₀ = 0,2 м/с.

Решение. В постановке дайной задачи идет речь о конечном перемещении системы, поэтому следует применить теорему об изменении кинетической энергии в интегральной форме:

.

Кинетическая энергия системы получена в предыду­щей задаче

,

где т_пр = 6280 кг — приведенная к кузову масса системы. Начальная кинетическая энергия системы

Дж.

Вычислим теперь величину работы действующих сил (рис. 63).

Внешние силы. Силы тяжести барабанов G ₂ и кузова G ₁ работы не совершают, поскольку они перпендикуляр­ны скоростям (и, соответственно, перемещениям) точек их приложения. Также не работают нормальные реакции R_n и R’_n и силы трения F_rp и 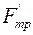, так как всегда равны нулю скорости их точек приложения — мгновенных центров скоростей, и, соответственно, постоянно равны нулю их мощности.

Работу будут совершать моменты сопротивления каче­нию:

и ,

а именно:

,

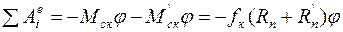где

.

Здесь φ — угол поворота барабанов, для которого, ин­тегрируя уравнение кинематической связи ω = v/r с уче­том нулевых начальных условий для перемещений s и φ, легко получаем φ = s/r. Тогда

.

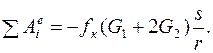Внутренние силы. Запишем, учитывая, что кузов не вращается, суммарную работу внутренних сил (моментов) М и М ’:

.

Тогда сумма работ всех сил запишется в виде

.

Множитель, стоящий в этой формуле перед перемеще­нием s, — это приведенная сила системы

Итак

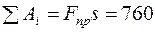Дж.

Собирая правую и левую части теоремы, получаем

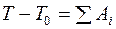
или Т – 125,6 = 760, откуда

и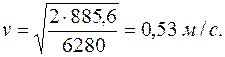

Дата добавления: 2014-01-06