Потенциальное силовое поле и потенциальная энергия

Теорема в интегральной (конечной) форме. Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, приложенных к системе, на том же перемещении.

Доказательство: Запишем теорему в интегральной форме для k - й точки системы:

,

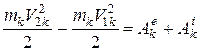где 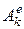и 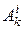— соответственно работа внешней и внутренней сил, приложенных к k -й точке, на некотором перемещении.

Суммируя по всем точкам системы, получим

Для системы твердых тел 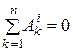(по свойству внутренних сил). Тогда

.

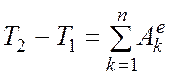Задача 2. Каток А приводится в движение из состояния покоя по­средством троса, который одним концом намотан на каток, а вто­рым — на барабан В. Каток А считать однородным цилиндром массы 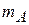= 50 кг и радиуса 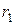= 0,4 м. Масса барабана 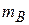= 20 кг распределена по его ободу радиуса 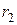= 0,2 м. К барабану при­ложен вращающий момент = 100 Нм. Пренебрегая сколь­жением и трением качения катка по горизонтальной плоскости и весом троса, определить скорость катка, когда он переместится на расстояние s = 2 м.

Решение. Применим теорему об изменении кинетической энергии механической системы в интегральной форме:

,

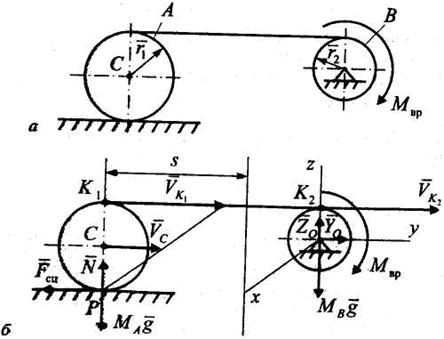
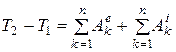где 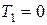— система движется из состояния покоя

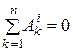— по свойству внутренних сил. Тогда 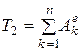. . 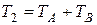Каток А совершает плоскопараллельное движение.

.

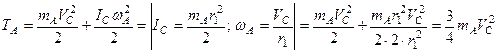Барабан В совершает вращательное движение.

.

.

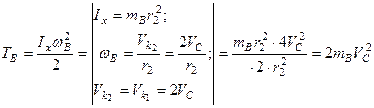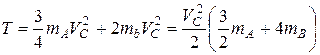Внешними силами являются силы тяжести 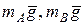, нормальная реакция 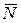, сила сцепления 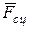, вращающий мо­мент , реакци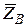и и .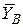

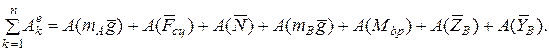
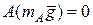так как сила 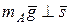; 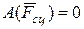так как сила 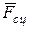приложена в МЦС; 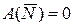так как 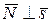; 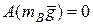, , 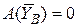— точка приложения сил не перемещается.

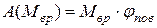, где .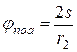

Тогда

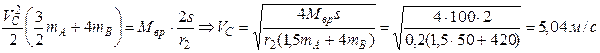
Силовым нолем называется часть пространства, в каждой точке которого на материальные точки действуют силы, зави­сящие от координат и времени, т. е.

.

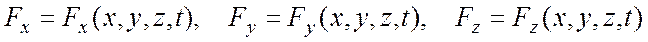Стационарное силовое поле — поле, в котором силы не за­висят от времени.

Потенциальное силовое поле — стационарное поле, в кото­ром работа силы не зависит от формы траектории перемеще­ния точки ее приложения. Такие силы называются потенци­альными или консервативными. Это сила тяжести, сила упру­гости.

Потенциальная энергия П точки или механической системы — это энергия покоя, которая представляет собой работу, совер­шаемую потенциальными силами при перемещении матери­альной точки или механической системы из заданного поло­жения в некоторое нулевое положение (в нулевой уровень) — положение, в котором потенциальная энергия равна нулю.

Консервативная система — это механическая система, в ко­торой действуют только потенциальные силы.

Проекции силы на оси декартовых координат в потенци­альном силовом поле

.

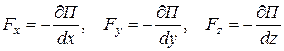Элементарная работа силы в потенциальном силовом поле

,

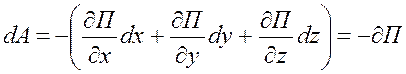т. е. равна со знаком (-) полному дифференциалу от потенциальной энергии.

Работа силы на некотором перемещении в потенциальном силовом поле

,

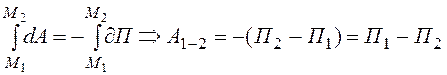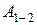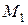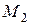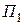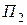где — работа по перемещению из положения в поло­жение , и — потенциальная энергия соответственно в этих положениях.

Задача 3. Груз массы т = 10 кг находит­ся на высоте 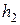= 1 м от стола. Высота стела 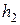= 0,5 м. Опреде­лить потенциальную энергию гру­за, по отношению к столу и по отношению к полу, принимая их за нулевой уровень.

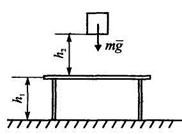
Решение. По отношению к столу

.

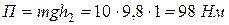По отношению к полу

.

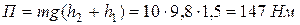Задача 4.. На середину упругой балки жесткости с = 39,2 Н/см, закрепленной по концам, положили груз массы 100 кг, под дей­ствием которого балка прогнулась на величину 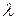= 25 см. Определить потенциальную энергию консервативной системы.

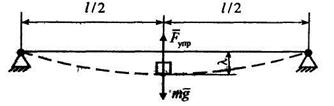
Решение. Примем за нулевой уровень ось балки до деформации

.

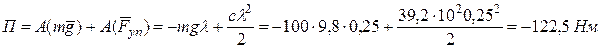Дата добавления: 2014-01-06