
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебра логики
|
|
|
|
ДАННЫЕ
Данные – это зарегистрированные сигналы.
Существуют различные физические методы регистрации данных (изменение магнитных, оптических характеристик поверхностей, состояния электронной системы, химического состава и т.д.). В зависимости от используемого метода регистрации применяются различные типы носителей (бумага, CD-ROM, магнитные диск и лента, триггеры).
Операции с данными:
- сбор данных;
- формализация данных;
- фильтрация данных;
- сортировка данных;
- архивация данных;
- защита данных;
- транспортировка данных;
- преобразование данных.
Последняя операция – важнейшая. Эта операция связанна с переводом данных из одной формы в другую. Преобразование данных необходимо, во – первых, для того, чтобы компьютер или человек мог хранить и обрабатывать данные в удобной для них форме. Во-вторых, многократное преобразование данных необходимо при их транспортировке. В ходе преобразования данных из одной формы представления к другой проводится операция кодирования. Кодирование применяется в различных областях (система записи математических объектов, азбука Морзе, система Брайля для слепых, морская сигнализация флажками и т.д.).
Следует отметить, что в каждой области человеческой деятельности существует множество других, часто весьма специфических операций с данными, которые выполняются в ходе решения различных задач социальной, экономической, научной, промышленной, культурной направленностей.
Данные и информация, грубо говоря, связаны следующим образом: информация – это полезное содержание данных, данные – это форма представления информация. Более полная характеристика указанной связи обеспечивается выделением трех аспектов информации: прагматического, семантического и синтаксического. Прагматический аспект отражает соответствие информации цели, для которой ее предполагает использовать потребитель информации. Семантический аспект отражает степень соответствия объекта и его образа, содержащегося в информации (данных), т.е. речь идет о смысловом содержании информации. Синтаксический аспект затрагивает форму представления информации, но не ее смысловое содержание. Можно сказать, что данные представляют собой информацию в синтаксическом аспекте.
Высказывание – повествовательное предложение, относительно которого определенно и объективно можно сказать истинно оно или ложно (ЛОЖЬ или ИСТИНА, 0 или 1, TRUE или FALSE). Алгебра логики – раздел математики, изучающий процессы умозаключений и законы, которые позволяют из истинности одних высказываний делать заключения об истинности или ложности других высказываний, независимо от их конкретного содержания. Алгебра логики (булева алгебра) была создана в 1854 г. Дж. Булем и в настоящее время находит широкое применение при разработке алгоритмов и для структурно-функционального описания, анализа и синтеза современных электронных схем.
Базовыми операциями алгебры логики служат операции логического умножения – конъюнкции (обозначается точкой или знаком 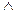 ), логического сложения – дизъюнкции (обозначается знакам + или
), логического сложения – дизъюнкции (обозначается знакам + или 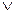 ), логического отрицания – инверсии (обозначается надчеркиванием или знаком
), логического отрицания – инверсии (обозначается надчеркиванием или знаком 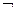 ). При составлении формул применяются скобки, чтобы изменять порядок выполнения операций. Наивысшим приоритетом обладает операция инверсии, затем идет конъюнкция и потом уже дизъюнкция.
). При составлении формул применяются скобки, чтобы изменять порядок выполнения операций. Наивысшим приоритетом обладает операция инверсии, затем идет конъюнкция и потом уже дизъюнкция.
Таблицы истинности для указанных операций:
| А | 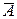
|
| А | В | А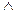 В В
|
| А | В | А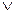 В В
|
Представляют интерес еще две логические операции: эквиваленции (обозначается знаком 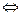 ) и импликации (обозначается знаком
) и импликации (обозначается знаком 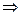 ).
).
| А | В | А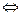 В В
|
| А | В | А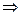 В В
|
Приведем основные логические законы (тождественно истинные высказывания), которые позволяют упрощать формулы, заменяя их подформулы эквивалентными выражениями:
1. 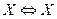 - закон тождества
- закон тождества
2. 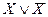 - закон исключенного третьего
- закон исключенного третьего
3. 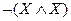 - закон противоречия
- закон противоречия
4. 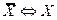 - закон двойного отрицания
- закон двойного отрицания
5. 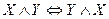 - закон коммутативности конъюнкции
- закон коммутативности конъюнкции
6. 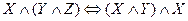 - закон ассоциативности конъюнкции
- закон ассоциативности конъюнкции
7. 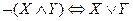 и
и 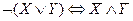 - законы де Моргана
- законы де Моргана
8. 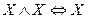 и
и 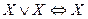 - законы сокращений
- законы сокращений
9. и еще с десяток тождественно истинных и тождественно ложных высказываний.
Пример 1. Упростить логическую формулу
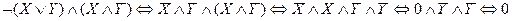
Пример 2. Доказать законы де Моргана, построив соответствующие таблицы истинности.
| X | Y | 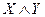
| 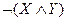
| 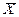
| 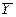
| 
| 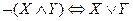
|
Таким образом, результат, выражаемый последним столбцом таблицы, свидетельствует, что высказывание 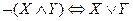 является тождественно истинным (выполняется при любых комбинациях значений входящих в него высказываний), т.е. оно действительно является логическим законом. Так же доказывается второй закон де Моргана.
является тождественно истинным (выполняется при любых комбинациях значений входящих в него высказываний), т.е. оно действительно является логическим законом. Так же доказывается второй закон де Моргана.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 433; Нарушение авторских прав?; Мы поможем в написании вашей работы!