Переход от одного опорного плана к другому опорному плану

Метод последовательного улучшения плана

Метод основан на упорядоченном переборе угловых точек множества планов задачи в сторону увеличения (или уменьшения) линейной формы и содержит три существенных момента.

Во-первых, указывается способ вычисления опорного плана. Во-вторых, устанавливается, признак, который позволяет проверить, является ли выбранный опорный план оптимальным. В третьих приводится способ, позволяющий по выбранному неоптимальному опорному плану построить другой опорный план, более близкий к оптимальному.

Рассмотрим ЗЛП в канонической форме

, (10.1)

где - матрица условий размером

Пусть ранг матрицы условий равен . Пусть все опорные планы задачи являются невырожденными и - произвольный опорный план с базисом 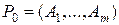. Т.е. считаем первые компонент точки положительными. Так как точка принадлежит 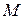, то ее координаты удовлетворяют системе ограничений

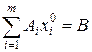. (10.2)

Так как вектора 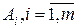составляющие базис - линейно независимы, то существуют 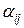не все равные нулю, такие что

Разложим вектор 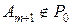по базису .

(10.3)

Умножим обе части последнего соотношения на некоторую величину , и результат вычтем из (10.2)

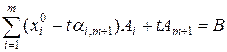. (10.4)

Отсюда следует, что точка

удовлетворяет ограничениям типа равенств задачи (10.1). Чтобы эта точка 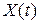являлась планом задачи необходимо выполнение условий неотрицательности её координат

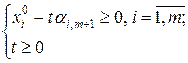(10.5)

При этом,

· если все , то (10.5) выполняется при любом

· если же существует 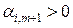, то (10.5) будет выполняться не при любом значении .

Решая неравенства 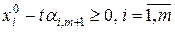относительно , получим

.

Ясно что, таких чисел может быть больше одного. Выберем наименьшее из них и обозначим его , т.е.

.

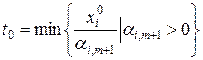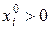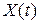Так как план невырожденный и следовательно, , то . Итак, чтобы точка принадлежала множеству планов ЗЛП 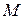, нужно брать из полуинтервала . Однако при точка 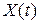содержит положительных координат и, следовательно, не является угловой. План 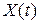может быть опорным лишь при таком , при котором одна из его компонент обратиться в ноль. Очевидно, это произойдет при .

Пусть для определенности

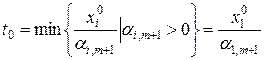
Тогда первая координата 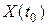обратиться в ноль

,

т.е. 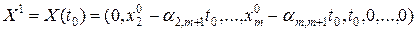имеет ровно положительных координат.

Покажем, что - опорный план ЗЛП. Для этого нужно показать, что столбцы 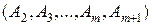образуют линейно – независимую систему векторов.

Допустим противное, т.е., что вектора 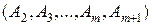- линейно зависимы. Тогда существует

. (10.6)

С другой стороны, мы уже знаем, что

(10.7)

Подставим выражение (10.7) в предыдущее равенство (10.6)

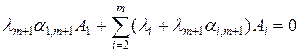(10.8)

Так как система 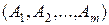- линейно независима равенство (10.8) возможно только в случае, когда все коэффициенты линейной комбинации равны нулю

Учитывая, что 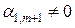, то из последних соотношений получаем 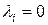, , что противоречит предположению о линейной зависимости, а значит, - опорный план ЗЛП (10.1).

Базис этого опорного плана получился, очевидно, из базиса 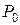исходного опорного плана путем введения в него вектора и удаления вектора . Таким образом, мы перешли от одного опорного плана к другому опорному плану 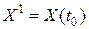. Этот переход был выполнен с помощью процедуры однократного замещения, т.е. из старого базиса 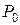был выведен вектор-столбец и введен .

Рис 10.3.

Ребро, соединяющее соседние угловые точки и . определяется угловой точкой и вводимым в базис вектором 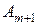. Если бы вместо 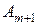ввели бы другой вектор, то получили бы другое ребро, а, следовательно, и другую угловую точку (рис 10.3).

Замечание 1. Если не выполняются условия, наложенные на коэффициент разложения вектора 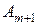по начальному базису, т.е. если , , то не удастся подобрать такое , чтобы одна из базисных координат обратилась в ноль. Значит, ребро 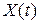не будет иметь другой вершины, т.е. оно является неограниченным лучом. Т.е. множество 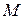неограниченно.

Замечание 2. Если является вырожденным опорным планом, то может достигаться при нескольких 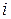, в этом случае, вектор, выводимый из базиса, определяется неоднозначно. Новый опорный план получится вырожденным и в зависимости от того, какой вектор выводится, будут получаться различные базисы одного и того вырожденного опорного плана 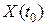, что приводит к образованию так называемого зацикливания алгоритма последовательного улучшения плана.

Процесс получения нового опорного плана заключается в выборе вектора, который подлежит введению в базис и определении вектора подлежащего исключению из базиса.

Критерий, используемый для определения вектора, подлежащего включению в базис, является основным элементом симплекс-метода.

Дата добавления: 2014-01-06