Графический метод решения ЗЛП

Рассмотрим ЗЛП в канонической форме: .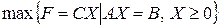

Пусть 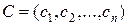- ненулевой вектор, тогда линейная форма задачи задает в пространстве 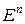семейство параллельных гиперплоскостей линейной формы 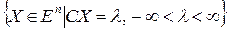, нормальным вектором которых является вектор C. Если 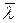- фиксированное значение, то гиперплоскость делит все пространство на два полупространства: нижнее и верхнее .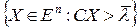

Если существует : 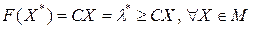, то - оптимальный опорный план. Гиперплоскость 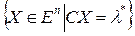- опорная гиперплоскость множества М в точке . Причем по отношению к опорной гиперплоскости все множество М находится в нижнем полупространстве, т.к. . Поэтому для графического решения задачи необходимо найти опорную гиперплоскость, по отношению к которой все множество М находится в нижнем полупространстве.

Таким образом, графический метод решения ЗЛП заключается в перемещении гиперплоскости линейной формы из некоторого начального положения по направлению вектора С до такого положения, когда при дальнейшем смещении гиперплоскость уже не будет иметь общих с множеством М точек. Пересечение опорной гиперплоскости с множеством М и будет является решением ЗЛП.

Для того чтобы решить графически ЗЛП необходимо выполнить следующие действия.

1. Построить множество допустимых планов задачи. В общем случае оно представляет собой выпуклый многогранник. Если ограничения в задаче несовместны, множество допустимых планов является пустым множеством, а задача поиска экстремума не имеет смысла.

2. Построить вектор С с началом в некоторой точке .

3. Построить гиперплоскость линейной формы (линию уровня) проходящую через точку .

4. Передвигать гиперплоскость линейной формы параллельно самой себе в направлении вектора C (так как вектор 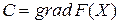задает направление возрастания F(X)) до получения опорной гиперплоскости.

Замечание. В случае непустого множества допустимых планов возможны три типовых ситуации:

а) опорная гиперплоскость касается множества допустимых планов в одной точке (задача имеет единственное решение);

б) опорная гиперплоскость касается множества допустимых планов вдоль стороны многоугольника (задача имеет бесконечное множество решений);

в) опорная гиперплоскость не определяется (задача не имеет решения).

Пример 10.1. Решить графически двумерную задачу линейного программирования:

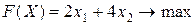
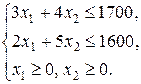
1. Легко проверить, что четырехугольник 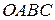на рис 10.1 является областью содержащей точки, для которых выполнены все ограничения задачи. Точки, лежащие внутри и на границе этой области являются допустимыми планами.

2. Построим вектор , с началом в некоторой точке D с координатами (100; 100). Очевидно, что вектор С, в силу линейности функции 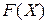будет перпендикулярен линиям уровня.

3. Построим линию уровня, проходящую через выбранную точку D. Подставим координаты точки D в целевую функцию 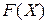: . Уравнение линии уровня, соответствующей данному значению 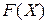будет иметь следующий вид . Построим полученную прямую (на рис.10.1 она обозначена (3')).

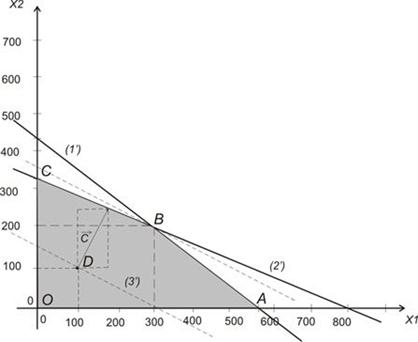
Рис.10.1.

4. Перемещая гиперплоскость линейной формы (линию уровня) из начального положения по направлению вектора С находим крайнее положение, определяющее опорную гиперплоскость. Поскольку полученная нами опорная гиперплоскость пересекается с множеством М в точке В, то наша задача имеет единственное решение.

Точка расположена на пересечении двух прямых (1') и (2'), поэтому, чтобы найти ее координаты необходимо решить следующую систему уравнений:

Таким образом - точка, соответствующая оптимальному решению задачи со значением функции .

Пример 10.2. Решим графически двумерную задачу линейного программирования:

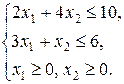
1. Окрашенная область ОАВС на рис.10.2 – множество допустимых планов ЗЛП.

2. Построим вектор С с началом в точке принадлежащей множеству допустимых планов, например, в точке D с координатами (1; 1).

3. Уравнение линии уровня проходящей через точку D будет иметь вид: 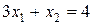. Построим полученную прямую (на рис.10.2 она обозначена (3')).

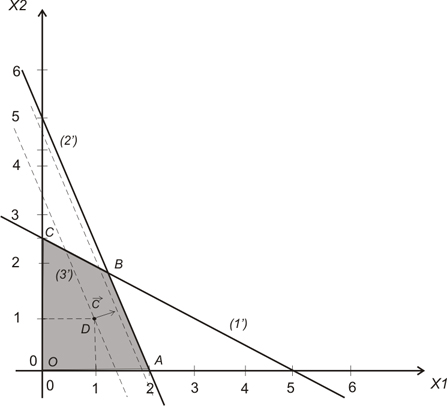
Рис 10.2.

4. Перемещая гиперплоскость линейной формы (линию уровня) из начального положения (3') по направлению вектора С находим крайнее положение, определяющее опорную гиперплоскость. Поскольку полученная нами гиперплоскость пересекается с множеством М по ребру АВ, то наша задача имеет бесконечное множество решений. А именно, все точки отрезка АВ являются оптимальными планами задачи, на которых достигается максимальное значение линейной формы .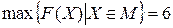

Дата добавления: 2014-01-06