Постановка задачи одномерной оптимизации

МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Изложение методов оптимизации начнем с рассмотрения простейшей математической модели оптимизации, в которой целевая функция зависит от одной переменной. Такие задачи возникают при изучении объектов, зависящих от одной скалярной переменной, когда требуется выбрать эту переменную наилучшим в том или ином смысле образом. Кроме того, эти задачи входят как составная часть во многие итерационные методы решения задач минимизации функций многих переменных и других более сложных экстремальных задач.

С задачами минимизации функций одной переменной мы впервые сталкиваемся при изучении начальных глав математического анализа и решаем их методами дифференциального исчисления. Может показаться, что задачи минимизации функций одной переменной достаточной просты и методы их решения хорошо разработаны и изучены. Однако это не совсем так. Оказалось, что методы дифференциального исчисления находят ограниченное применение и далеко не всегда удобны для реализации в компьютерных программах. Хотя в последнее время и появились другие, более удобные для реализации, методы, но, тем не менее, эту область экстремальных задач нельзя считать завершенной. Мы остановимся на некоторых наиболее известных методах, достаточно хорошо проявивших себя на практике.

Пусть функция определена на некотором множестве U вещественной оси 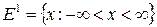. Поскольку максимизация целевой функции 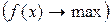эквивалентна минимизации противоположной величины 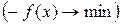, будем рассматривать только задачу минимизации функции на множестве U. Начнем с того, что уточним постановку этой задачи. Для этого напомним некоторые основные понятия.

Определение 2.1. Число называется точкой глобального (абсолютного) минимума или просто точкой минимума функции на множестве U, если для всех 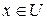. Значение 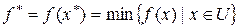называется глобальным (абсолютным) минимумом или просто минимумом функции на U. Множество всех точек минимума функции на U будем обозначать через .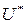

Определение 2.2. Число называется точкой локального минимума функции на U, если для всех 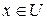, достаточно близких к , т.е. если существует число 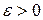такое, что это неравенство выполняется для любого .

В зависимости от свойств множества U и функции множество 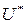может содержать одну, несколько или даже бесконечно много точек. Также возможны случаи, когда 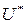пусто.

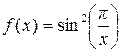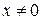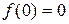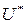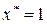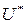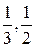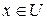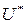Пример 2.1. Пусть при и . На множестве минимальное значение равно нулю, а множество состоит из единственной точки . Если , то содержит три точки , 1. В случае функция не имеет наименьшего значения на U. В самом деле, какую бы точку мы не взяли, найдется точка из U такая, что значение в ней будет меньше . Это значит, что пусто.

Пример 2.2. Пусть . Минимальное значение на U равно нулю, множество 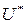состоит из единственной точки.

Пример 2.3. Пусть 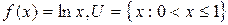. Здесь 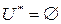, т.к. во всех точках из U функция принимает конечные значения, а для последовательности 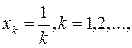имеем .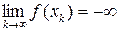

В примерах 2.1–2.2 функции ограничены снизу на рассматриваемых множествах, а в примере 2.3 функция не ограничена снизу.

Определение 2.3. Функция называется ограниченной снизу на множестве U, если существует число M такое, что 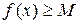для всех .

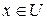В тех случаях, когда 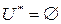, естественным обобщением понятия наименьшего значения функции является понятие нижней грани функции.

Определение 2.4. Пусть функция ограничена снизу на множестве U. Тогда число называется точной нижней гранью функции на множестве U, если 1) 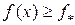при всех 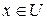; 2) для любого сколь угодно малого числа 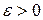найдется точка 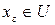такая, что .

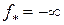Если функция неограниченна снизу на U, то в качестве нижней грани на U принимается . Точную нижнюю грань на U обозначают через .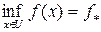

В примерах 2.1–2.2 нижняя грань 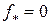, а в примере 2.3 .

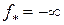Если , то, очевидно, нижняя грань на U совпадает с наименьшим значением 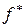этой функции на U, т.е. . В этом случае говорят, что функция на U достигает своей нижней грани. Отметим, что 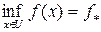всегда существует, а 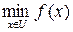, как видно из примеров 2.1–2.3 не всегда имеет смысл.

Пример 2.4. Пусть 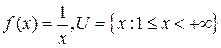. Покажем, что функция на U не имеет точек минимума, а точная нижняя грань существует.

Предположим, , т.е. существует хотя бы одна точка 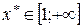такая, что для всех 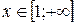. Выберем произвольное число 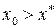. Очевидно , причем 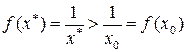, что противоречит предыдущему неравенству. Поэтому исходное предположение неверно и .

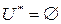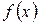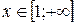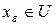Убедимся в том, что число 0 является точной нижней гранью данной функции на U. В самом деле, для всех имеем , т.е. число 0 удовлетворяет первому из неравенств в определении 2.4. Далее пусть . Возьмем произвольное . Тогда, очевидно, и 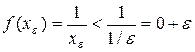, т.е. для числа 0 выполняется и второе неравенство из определения точной нижней грани. Поэтому .

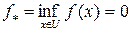Если множество точек минимума функции на U пусто, то задача минимизации теряет смысл. В этом случае можно ограничиться поиском точки 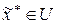, в которой значение с заданной погрешностью ε приближает точную нижнюю грань функции на множестве U, т.е. .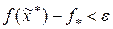

Определение 2.5. Последовательность точек 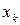из U называется минимизирующей последовательностью для функции на множестве U, если .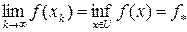

Из определения и существования точной нижней грани следует, что минимизирующая последовательность всегда существует.

Теперь можем перейти к формулировке постановки задачи одномерной оптимизации как задачи минимизации функции на множестве U.

Условимся, что запись

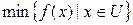
(2.1)

или, ей эквивалентная 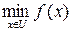будет означать, что ставится задача определения величины 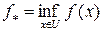. Причем в задаче (2.1) неважно, будет ли множество 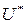точек минимума на U непустым, или оно пусто. В случае, когда множество 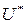непусто, требуется наряду с найти точку .

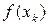Заметим, что получить точное решение поставленной задачи (2.1) удается лишь в редких случаях. Поэтому на практике при решении задачи (2.1) обычно строят минимизирующую последовательность для функции на U и затем в качестве приближения для берут величину при достаточно большом k. В случае непустого множества 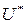достаточно построить минимизирующую последовательность , которая сходится к множеству 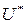. Один достаточно широкий класс функций, для которых , определяет известная теорема Вейерштрасса, согласно которой функция, непрерывная на замкнутом ограниченном множестве, достигает на этом множестве своих максимального и минимального значений. Таким образом, задача (2.1) с непрерывной целевой функцией на U всегда имеет решение.

Если функция на множестве U имеет, кроме глобального, локальные минимумы, отличные от него, то минимизация , как правило, сильно затрудняется. Многие методы поиска точки минимума приспособлены только для функций, у которых каждый локальный минимум является одновременно и глобальным. Этим свойством обладают унимодальные функции.

Дата добавления: 2014-01-06