Выпуклые функции

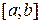Определение 2.7. Функция , заданная на отрезке , называется выпуклой на этом отрезке, если для всех 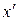, 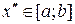и произвольного числа 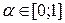выполняется неравенство

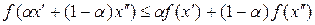. (2.3)

Перечислим основные свойства выпуклых функций.

1. Если функция выпукла на 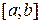, то на любом отрезке 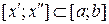ее график расположен не выше хорды, проведенной через точки графика с абсциссам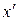и и 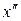(рис. 2.2).

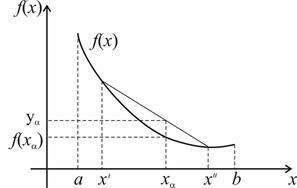
Рис. 2.2. Взаимное расположение графика выпуклой функции и хорды

Из курса математического анализа известны следующие условия выпуклости функции:

2. Для того чтобы дифференцируемая на отрезке 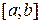функция была выпуклой на этом отрезке, необходимо и достаточно, чтобы производная 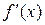не убывала на ;

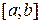3. Для того чтобы дважды дифференцируемая на отрезке 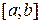функция была выпуклой на этом отрезке, необходимо и достаточно, чтобы при всех 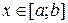выполнялось неравенство .

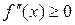4. Условие выпуклости для дифференцируемой на отрезке 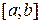функции означает, что на этом отрезке любая касательная к графику лежит не выше этого графика (рис. 2.3).

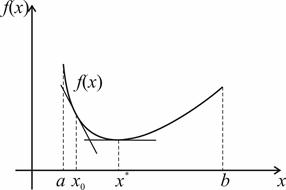
Рис. 2.3. Взаимное расположение графика выпуклой дифференцируемой

функции и касательной к нему

5. Если - выпуклая дифференцируемая на отрезке 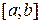функция и в точке 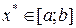выполняется равенство

, (2.4)

то 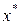является точкой глобального минимума на .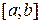

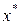Благодаря свойству 4 выпуклых функций данное свойство приобретает простой геометрический смысл: поскольку касательная к графику в точке с абсциссой горизонтальна, а этот график расположен не ниже касательной, то 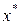есть точка минимума (рис. 2.3).

Таким образом, равенство (2.4) для выпуклой дифференцируемой функции является не только необходимым условием глобального минимума (как для всякой дифференцируемой функции), но и его достаточным условием.

Замечание 1. Можно показать, что всякая выпуклая непрерывная на отрезке 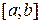функция является и унимодальной на этом отрезке. Обратное, вообще говоря, неверно (рис. 2.4).

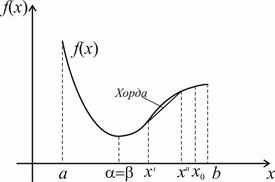
Рис. 2.4. График унимодальной, но не выпуклой функции

Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функции.

Замечание 2. При исследовании выпуклости функций на практике неравенство (2.3) удается использовать только в редких случаях. Поэтому для дифференцируемых достаточное число раз функций обычно применяют дифференциальные критерии выпуклости (см. свойства 2 и 3 выпуклых функций).

Замечание 3. Непосредственная проверка унимодальности с помощью определения 2.6 также в большинстве случаев вызывает затруднения, и для обоснования унимодальности достаточно гладких функций часто используют те же дифференциальные критерии выпуклости (свойства 2 и 3). Если функция оказывается выпуклой, то можно утверждать (замечание 1), что она унимодальна. Разумеется, при отрицательном результате проверки функции на выпуклость нельзя сделать вывод о том, что она не унимодальна.

Дата добавления: 2014-01-06