
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод ломаных
|
|
|
|
Рассмотренные ранее методы одномерной оптимизации существенно используют свойство унимодальности минимизируемой функции 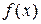 . Если же функция
. Если же функция 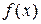 этим свойством не обладает, т.е. является полимодальной, то погрешности в определении минимального значения и точек минимума функции могут быть значительными.
этим свойством не обладает, т.е. является полимодальной, то погрешности в определении минимального значения и точек минимума функции могут быть значительными.
Кроме того, применение этих методов приведет, вообще говоря, лишь в окрестность точки локального минимума, в которой значение функции может сильно отличаться от искомого минимального значения на отрезке. Поэтому представляется важным разработка методов поиска глобального минимума, позволяющих строить минимизирующие последовательности для функций, не обязательно являющихся унимодальными.
Одним из таких методов минимизации полимодальных функций является метод ломаных. Однако данный метод так же имеет ограничение, он применим для минимизации функций, удовлетворяющих условию Липшица на отрезке.
Для построения метода ломанных используются свойства липшицевых функций (см. определение 2.8 и свойства 1-5 там же).
Этот метод начинается с выбора произвольной точки 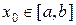 в качестве начальной и составления вспомогательной функции
в качестве начальной и составления вспомогательной функции  , определенной на всем отрезке
, определенной на всем отрезке  . Очевидно, что функция
. Очевидно, что функция 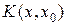 кусочно-линейна на
кусочно-линейна на  и что график ее представляет собой ломаную линию, составленную из отрезков двух прямых, имеющих угловые коэффициенты
и что график ее представляет собой ломаную линию, составленную из отрезков двух прямых, имеющих угловые коэффициенты 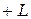 и
и 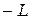 , и пересекающихся в точке
, и пересекающихся в точке 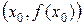 . Кроме того, при всех
. Кроме того, при всех 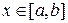 выполняется неравенство
выполняется неравенство 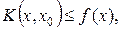 причем
причем  . Это значит, что график функции
. Это значит, что график функции 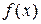 лежит выше ломаной
лежит выше ломаной 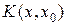 при всех
при всех 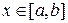 и имеет с ней общую точку
и имеет с ней общую точку 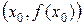 .
.
Следующая точка  определяется из условия
определяется из условия 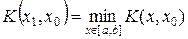 . В силу линейности функции
. В силу линейности функции 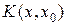 очевидно
очевидно  или
или 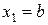 . Далее берется новая вспомогательная функция
. Далее берется новая вспомогательная функция 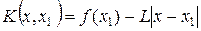 и строится аппроксимирующая функция
и строится аппроксимирующая функция 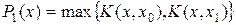 . Очередная точка
. Очередная точка 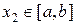 находится из условия
находится из условия  . Далее строятся новые функции
. Далее строятся новые функции 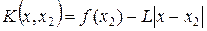 и
и  и точка
и точка  такая, что
такая, что  . Итак далее (см. рис. 3.4)
. Итак далее (см. рис. 3.4)
Пуст точки  ,
,  уже известны. Тогда составляется следующая функция
уже известны. Тогда составляется следующая функция 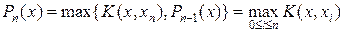 и следующая точка
и следующая точка 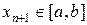 определяется из условия
определяется из условия
 . (3.9)
. (3.9)
Если минимум 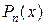 на
на 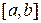 достигается в нескольких точках, то в качестве
достигается в нескольких точках, то в качестве  можно взять любую из них. Метод ломаных описан.
можно взять любую из них. Метод ломаных описан.

|
Рис. 3.4. 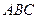 - график - график  , ,  - график - график 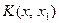 , , 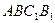 - график - график  , ,
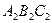 - график - график 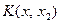 , ,  - график - график 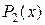 , , 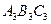 - график - график 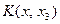 , , 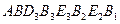 - график - график 
|
Очевидно, что 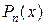 есть кусочно-линейная функция, график которой представляет собой непрерывную линию, состоящую из отрезков прямых с угловыми коэффициентами + L и – L.
есть кусочно-линейная функция, график которой представляет собой непрерывную линию, состоящую из отрезков прямых с угловыми коэффициентами + L и – L.
Таким образом, на каждом шаге метода ломанных задача минимизации функции  заменяется более простой задачей минимизации кусочно-линейной функции
заменяется более простой задачей минимизации кусочно-линейной функции  , которая приближает функцию
, которая приближает функцию  снизу, причем
снизу, причем  монотонно возрастают.
монотонно возрастают.
Таким образом, с помощью метода ломаных можно получить решение задачи одномерной оптимизации (2.1) для функций удовлетворяющих условию Липшица. Этот метод не требует унимодальности функции, и более того, функция может иметь сколько угодно точек локального минимума на рассматриваемом отрезке. На каждом шаге метода ломаных нужно минимизировать кусочно-линейную функцию 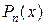 , что может быть сделано простым перебором известных вершин ломаной
, что может быть сделано простым перебором известных вершин ломаной 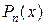 . При этом перебор существенно упрощается благодаря тому, что ломаная
. При этом перебор существенно упрощается благодаря тому, что ломаная 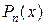 отличается от ломаной
отличается от ломаной  не более чем двумя новыми вершинами. К достоинствам метода относится и то, что он сходится при любом выборе начальной точки
не более чем двумя новыми вершинами. К достоинствам метода относится и то, что он сходится при любом выборе начальной точки 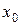 .
.
Отметим, что метод ломаных не возможно реализовать без знания константы Липшица  . При определении константы Липшица можно непосредственно использовать определение 2.8 и замечания 1-5, приведенные вслед за этим определением. На практике, часто для оценки минимальной константы
. При определении константы Липшица можно непосредственно использовать определение 2.8 и замечания 1-5, приведенные вслед за этим определением. На практике, часто для оценки минимальной константы  вычисляют угловые коэффициенты некоторого числа хорд, соединяющих точки графика минимизируемой функции. Максимальный из модулей этих коэффициентов является приближением снизу к
вычисляют угловые коэффициенты некоторого числа хорд, соединяющих точки графика минимизируемой функции. Максимальный из модулей этих коэффициентов является приближением снизу к  , причем тем лучшим, чем меньше эти хорды.
, причем тем лучшим, чем меньше эти хорды.
Следует иметь в виду, что использование завышенной оценки для  ухудшает сходимость метода ломаных, приводит к излишне большому количеству вычислений значений минимизируемой функции. Если же пользоваться заниженной оценкой для
ухудшает сходимость метода ломаных, приводит к излишне большому количеству вычислений значений минимизируемой функции. Если же пользоваться заниженной оценкой для  , то метод может привести к неправильному определению приближения минимального значения.
, то метод может привести к неправильному определению приближения минимального значения.
Контрольные вопросы
1. Какие методы называют прямыми методами минимизации?
2. Поясните достоинства и недостатки прямых методов минимизации.
3. Перечислить основные методы одномерного поиска.
4. Опишите метод равномерного поиска.
5. Как оценивается погрешность определения точки минимума функции методом равномерного поиска?
6. Какие возможности улучшения метода перебора реализованы в методе поразрядного поиска?
7. Приведите описание алгоритма метода поразрядного поиска.
8. Каков принцип построения методов исключения отрезков.
9. Чем выгодно отличаются методы исключения отрезков от методов перебора?
10. Опишите алгоритм метода деления отрезка пополам.
11. Как оценить число итераций метода дихотомии, необходимое для определения точки минимума с заданной точностью?
12. Какими особенностями обладает метод золотого сечения?
13. Какими достоинствами обладает метод ломаных в сравнении с другими методами одномерного поиска?
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 9458; Нарушение авторских прав?; Мы поможем в написании вашей работы!