Постановка задачи многомерной оптимизации

МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Исследование задач многомерной оптимизации сводится к поиску точек минимума функции многих переменных на всем пространстве соответствующей размерности. Такая задача сложнее задачи минимизации функции одной переменной, так как с ростом размерности пространства переменных возрастают объем вычислений и сложность алгоритмов, затрудняется анализ поведения целевой функции

Будем рассматривать функции многих переменных как функции, заданные в точках -мерного евклидова пространства . Точки представляются векторами-столбцами координат: 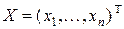, где символ «» - знак транспонирования. В дальнейшем, там где это не приводит к недоразумениям, символ «Т», будем опускать.

1. Точка 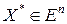называется точкой глобального минимума функции , если для всех выполняется неравенство . Значение называется минимумом функции. Множество всех точек глобального минимума функции будем обозначать через .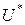

Замечание. Если , то вместо минимума функции иногда рассматривают ее точную нижнюю грань .

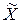2. Точка называется точкой локального минимума функции , если существует -окрестность точки :такая, что для всех выполняется неравенство .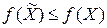

Теперь сформулируем постановку задачи безусловной оптимизации.

Дана целевая функция переменных , определенная не всем пространстве . Требуется определить минимум этой функции на и точки 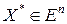в которых он достигается.

Условимся для обозначения данной задачи использовать следующую краткую стандартную запись:

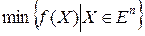(4.1)

или ей эквивалентную , .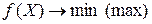

Классический метод решения задачи безусловной оптимизации

Под классическим методом решения поставленной задачи (4.1) понимается подход к поиску минимума функции, который основан на дифференциальном исчислении функций многих переменных.

Напомним некоторые понятия и факты, известные из курса математического анализа.

1. Если функция дифференцируема в точке , то ее приращение можно записать в виде

,

где - первый дифференциал в точке .

2. Вектор 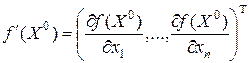называется градиентом функции в точке . В малой окрестности точки градиент указывает направление наискорейшего возрастания функции , а его норма характеризует скорость этого возрастания. Градиент в точке перпендикулярен линии (поверхности) уровня , проходящей через эту точку. Очевидно, 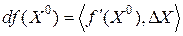, поэтому

(4.2)

3. Если функция дважды дифференцируема в точке , то

,

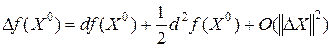где - второй дифференциал в точке .

Используя матрицу вторых производных (матрицу Гессе, гессиан) , второй дифференциал можно записать так: , поэтому

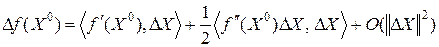. (4.3)

4. Из формул (4.2) и (4.3) следует, что для малых

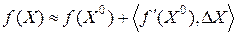(4.4)

или

(4.5)

т.е. в малой окрестности точки поведение дифференцируемой функции приближенно описывается формулой (4.4), а дважды дифференцируемой - формулой (4.5), причем представление (4.5) является более точным.

5. Если в точке функция дифференцируема и достигает локального минимума, то

или (4.6)

(необходимое условие минимума). Точки, в которых выполнено условие (4.6), называются стационарными точками дифференцируемой функции .

6. Если в стационарной точке функция дважды дифференцируема и матрица ее вторых производных 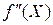положительно определена, то есть точка локального минимума (достаточное условие минимума).

Условия 5 и 6 лежат в основе классического метода минимизации функций, дифференцируемых во всем пространстве . Приведем алгоритм этого метода.

Шаг 1. Решив систему уравнений (4.6), найти все стационарные точки функции .

Шаг 2. Используя достаточные условия минимума, среди стационарных точек функции найти точки локального минимума и, сравнивая значения функции в них, определить точки глобального минимума.

Пример 4.1. Классическим методом решить задачу

.

Шаг 1. Запишем систему (3.12): ; ; 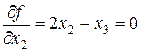. Решив ее, получим стационарную точку .

Шаг 2. Находим гессиан . Так как, согласно критерию Сильвестра, эта матрица положительно определена, заключаем, что является точкой минимума функции . Минимальное значение .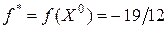

Замечание. Классический метод минимизации функций многих переменных имеет ограниченное практическое применение в основном из-за трудностей в аналитическом решении системы уравнений (4.6). Кроме того, на практике часто аналитическое задание функции неизвестно, а ее значения получаются в результате измерений. Все это вынуждает заняться разработкой других методов решения задачи (4.1) более удобных для компьютерной реализации.

Дата добавления: 2014-01-06