Метод циклического покоординатного спуска

Рассмотрим прямые методы решения задачи безусловной минимизации, использующие вместо итерационных процедур вида (4.7) простейшие вычислительные алгоритмы, основанные на рекуррентной формуле (4.13): 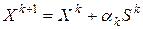, где 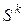- направление поиска точки 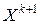из точки , а положительное число 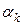- величина шага в этом направлении.

Способ выбора 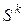и 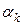будет определять одну из трёх рассматриваемых далее модификаций метода покоординатного спуска.

Метод циклического покоординатного спуска заключается в последовательной минимизации целевой функции 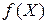сначала по направлению первого базисного вектора , затем второго - и т.д. После окончания минимизации по направлению последнего базисного вектора 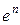цикл повторяется. Таким образом, метод циклического покоординатного спуска заключается в изменении каждый раз одной переменной, тогда как другие остаются постоянными.

Скорость сходимости данного метода невысока. Несмотря на это, метод циклического покоординатного спуска широко применяется на практике благодаря простоте реализации.

Заметим, что такой метод работает плохо, если в выражение минимизируемой функции входят произведения 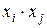, т.е. если имеет место взаимодействие между

Указанного недостатка можно избежать с помощью следующей модификации метода покоординатного спуска, известной под названием метода Зейделя.

Дата добавления: 2014-01-06