Основные правила получения тавтологий

Различают два основных правила образования тавтологий.

Правило 1. (правило заключения; правило отделения или правило modus ponens). Если формулы F и являются тавтологиями, то формула Н также является тавтологией.

Доказательство.

Докажем методом «от противного». Предположим, что существует набор значений переменных, при которых значение формулы Н = 0. Тогда, так как F = 1 (по условию формула F – тавтология), значение импликации 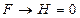. Получили противоречие с условием ( – тавтология и не может принимать значение 0). Следовательно, наше предположение неверно и формула Н является тавтологией.

Правило 2. (правило подстановки). Если формула F, содержащая пропозициональную переменную Х, является тавтологией, то подстановка в формулу F всюду вместо переменной Х любой формулы Н снова приводит к тавтологии. Новая формула при этом обозначается .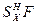

Пример 13: 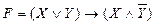(самостоятельно докажите, что она является тавтологией). Пусть 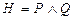. Тогда также является тавтологией (самостоятельно убедитесь в этом с помощью таблицы истинности).

Вопросы для контроля:

1. Высказывания. Высказывательные формы. Кванторы.

2. Логические связки. Логические операции.

3. Формулы логики высказываний.

4. Таблицы истинности.

5. Классификация формул логики высказываний.

6. Значение тавтологий.

7. Правила получения тавтологий.

Раздел 2. Логическая равносильность формул

Дата добавления: 2014-01-06