Расчет вспомогательных характеристик

t	Yt	ut	тt	dt	st	γt
	6,7	—	—	—	—
	7,3					+
	7,6					+
	7,9					+
	6,6			-1		-
б	8,6					+
	7,8					-
	7,7					-
	7,9					+
	8,2					+
	8,4					+
	9,1	г			1	+
	8,3					-
	8,7					+
	8,9					+
	9,1					+
	9,5					+
	10,4					+
	10,5					+
	10,2					-

1. Каждый уровень ряда Y_tсравнивается со всеми предыдущими, и определяются значения вспомогательных характеристик u_{t г} и m_t(графы 3, 4);

2. Находим d_t= u_t – m_t, s_t = u_t + m_tдля всех t, начиная со второго значения (графы 5, 6);

3.

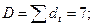
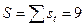
4. Значения µ, σ_S, σ_D для n= 20 берем из табл. 2.1:

µ= 5,195, σ_S = 1,677, σ_D = 2,279, тогда t_S = (9 - 5,195): 1,677 = 2,269 и t_D = 7: 2,279 = 3,07.

Значение t_aдля а= 0,05 берем из таблицы t-распределения Стьюдента: t _а = 2,093. Так как t_D> t _а и t_S> t_а,то с вероятностью 0,95 можно утверждать, что гипотеза об отсутствии тренда в среднем и в дисперсии отвергается, т. е. в исследуемом временном ряду существует тенденция развития.

П р и м е р 2.2. По данным предыдущего примера рассмотрим применение критерия „восходящих” и „нисходящих” серий.

1. В графе γ_t ставим „+”, если последующее значение больше предыдущего, и „-“ — если меньше (графа 7).

2. Определяем число серий:

ν(20) = 8.

3. Протяженность самой длинной серии

k_mах (20) = 6.

4. Табличное значение

k₀(20)=5

5. В соответствии с (2.1) делаем проверку:

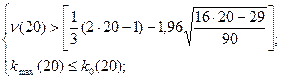
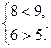
Отсюда видим, что второе неравенство не выполняется, следовательно, гипотеза об отсутствии тенденции отвергается, что подтверждает правильность вывода, сделанного в предыдущем примере.

Дата добавления: 2014-01-06