Механическое сглаживание

МЕТОДЫ ВЫДЕЛЕНИЯ ОБЩЕЙ ТЕНДЕНЦИИ ВРЕМЕННОГО РЯДА

После того как установлено (графически или с применением вышеописанных критериев), что временной ряд содержит тенденцию развития, необходимо определить поведение долговременной составляющей. Для этого применяются следующие методы, которые условно делятся на две группы:

1) методы механического выравнивания (сглаживания), основанные на том, что фактические уровни ряда заменяются расчетными, обладающими меньшей колеблемостью, чем исходные данные. В ряде случаев сглаживание ряда рассматривается как средство, помогающее определить, как выглядит тенденция развития;

2) методы аналитического выравнивания, основанные на том, что приблизительно известен вид тренда в аддитивном разложении (1.6). Рассматривая график временного ряда из примера (см. с. 10), можно предположить, что тенденция розничного товарооборота в регионе описывается линейной функцией времени t, т. е. F_t = a ₀ + а ₁t, где a ₀, а ₁ — неизвестные параметры, которые нужно определить (оценить).

В основе методов сглаживания трендовой составляющей (элиминирования случайных изменений в поведении временного ряда) лежит простая идея: если „индивидуальный” разброс значений временного ряда Y_t около своего среднего значения а характеризуется дисперсией σ², то разброс среднего из m членов временного ряда около того же значения а будет характеризоваться дисперсией, равной [1]. А уменьшение меры случайного разброса (дисперсии) и означает сглаживание соответствующей траектории.

Распространенным приемом выявления тенденции развития является сглаживание временного ряда с помощью простых и взвешенных скользящих средних.

Алгоритм сглаживания по простой скользящей средней можно представить в виде следующих этапов.

1. Для временного ряда Y_t определяют интервал сглаживания m, который включает в себя m последовательных уровней ряда (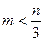). Выбор интервала сглаживания зависит от целей исследования. При этом надо иметь в виду, что чем шире интервал сглаживания, тем в большей степени погашаются колебания и тем плавнее получается тренд.

2. Рассчитываются средние арифметические из уровней ряда, входящих в интервал сглаживания.

3. Вычислив значение средней для первых m уровней, переходят к расчету средних для уровней у₂, у₃, у_m+2., затем для уровней у₃, у₄, у_m+2 и т. д. Таким образом, интервал сглаживания как бы скользит по временному ряду.

4. Заменяют фактические значения ряда, стоящие в центре интервала сглаживания, на соответствующие средние значения.

Если m — нечетное число (m = 2р + 1), то сглаженное значение относится к середине выбранного интервала и вычисляется по формуле

где 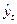— значение скользящей средней для момента t;

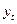— фактическое значение уровня в момент i (здесь i — порядковый номер уровня в интервале сглаживания).

Если m = 2р — четное число, тогда сглаженное значение будет находиться между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, которое заключается в нахождении двух скользящих сумм, определении скользящих средних по этим суммам и нахождении средней из средних (пример сглаживания ряда методом пятичленной и четырехчленной скользящей средней представлен в табл. 2.4, графы 3, 4, 5, 6).

Т а б л и ц а 2.4

Сглаживание урожайности зерновых культур в одном из хозяйств методом скользящей средней

Год	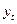, кг/га	5-летние скользящие средние	Скользящие4-летние суммы	Скользящие 4-летние средние нецентрированные	Центрированные скользящие средние	Взвешенные 5-летние скользящие средние
		—	—	—	—	—
	1 370	—	—	1 230	—	—
	1 210	1 250	—	1 320	1 280	1 280
	1 400	1 370	4 930	1 370	1 350	1 340
	1 320	1 410	5 300	1 460	1 410	1 410
	1 560	1 440	5 490	1 460	1 460	1 470
	1 540	1 520	5 890	1 570	1 510	1 510
	1 400	1 560	5 820	1 560	1 560	1 540
	1 760	1 470	6 260	1 450	1 500	1 560
	1 540	1 510	6 240	1 530	1 490	1 490
	1 090	1 530	5 790	1 470	1 500	1 430
	1 750	1 550	6 140	1 550	1 510	1 520
	1 500	1 520	5 880	1 630	1 580	1 620
	1 850	1 600	6 190	1 565	1 597	1 630
	1 420	—	6 520	—	—	—
	1 490	—	6 260	—	—	—

При работе с рядами квартальной и месячной динамики можно использовать следующие скользящие средние:

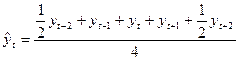
При использовании метода скользящих средних последние и первые р значений теряются, что является существенным недостатком этого метода, так как последние данные обладают наибольшей информативностью.

Для того чтобы восстановить потерянные значения в конце ряда, следует вычислить средний абсолютный прирост на последнем участке сглаживания путем его последовательного прибавления к последнему сглаженному уровню и тем самым получить недостающие р значений в конце временного ряда. Аналогичную процедуру можно реализовать для оценивания первых уровней ряда.

Если для исследуемого процесса характерно нелинейное развитие или для исследователя желательно сохранить мелкие волны, применение простой скользящей средней нецелесообразно. В этих случаях более надежным является применение взвешенной скользящей средней.

При сглаживании с помощью взвешенной скользящей средней на каждом участке выравнивание осуществляется по полиномам невысоких порядков (по параболам 2-го или 3-го порядка). Выравнивание по полиному 1-го порядка соответствует сглаживанию по простой скользящей средней. Взвешенная средняя приписывает каждому уровню вес, зависящий от удаления данного уровня от уровня, стоящего в середине интервала сглаживания (в отличие от простой скользящей средней, которая учитывает все уровни, входящие в интервал сглаживания, с равными весами). Выравнивание с помощью взвешенной скользящей средней осуществляется следующим образом.

Для каждого участка сглаживания подбирается полином вида

параметры которого оцениваются по методу наименьших квадратов (здесь i — порядковый номер уровня в пределах интервала сглаживания). Если отсчет времени в пределах участка сглаживания производить от его середины, т. е. i = -р, …, -2, -1, 0, 1, 2, …, р, то сглаженное значение уровня будет равно параметру а ₀ подобранного полинома. Весовые коэффициенты при уровнях ряда, входящих в интервал сглаживания, будут одинаковыми для всех участков. Причем при сглаживании по полиному k-й нечетной степени весовые коэффициенты будут такими же, как при сглаживании по полиному (k - 1)-степени.

Расчет взвешенных скользящих средних осуществляется по следующим формулам (полиномы имеют 2-ю или 3-ю степени, а m — нечетное число):

Как видно из приведенных формул, веса симметричны относительно центрального уровня у(и их сумма с учетом вынесенного за скобки общего множителя равна единице. Наличие в системе весов как положительных величин, так и отрицательных дает возможность сглаженной кривой сохранять различные изгибы.

Вычисленные значения взвешенных скользящих средних приведены в табл. 2.4 (см. графу 7).

Дата добавления: 2014-01-06