Аналитическое выравнивание временных рядов

Удобным средством описания временных рядов является их выравнивание с помощью тех или иных функций времени (кривых роста), которые позволяют получить выровненные (теоретические) значения уровней ряда 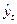. Аналитическое выравнивание состоит из двух основных этапов:

1) выбора типа кривой, форма которой соответствует характеру изменения временного ряда;

2) определения численных значений (оценивание) параметров кривой.

Для аналитического выравнивания временных рядов наиболее часто применяются относительно простые функции, которые условно можно разбить на три класса.

К 1-му классу относятся функции, используемые для описания процессов с монотонным характером развития и отсутствием пределов роста.

Ко 2-му классу относятся кривые, описывающие процесс, который в исследуемом периоде имеет предел роста. Функции, относящиеся к этому классу, называются кривыми насыщения.

Если кривые насыщения имеют точку перегиба, то их относят к 3-му классу кривых роста и называют S-образными кривыми.

Наиболее ответственным этапом при аналитическом выравнивании ряда является выбор формы кривой, образующей тенденцию, к которому можно подойти различными путями (графический метод, метод конечных разностей и т. д;). Однако какой бы путь ни был принят, он обязательно предполагает знакомство с основными свойствами кривых роста. Поэтому остановимся на характеристике отдельных кривых, наиболее часто применяемых на практике.

Среди кривых роста 1-го класса наиболее часто применяют полиномы (многочлены)

(2.3)

где а_i, — параметры многочлена (i = 0, 1, 2, …, р);

t — независимая переменная (время).

Коэффициенты многочленов невысоких степеней имеют конкретную интерпретацию в зависимости от содержания временного ряда. Например, их можно трактовать как скорость роста (а ₁), ускорение роста (а ₂), изменение ускорения (а ₃), а параметр a ₀ характеризует уровень ряда при t = 0. В экономических исследованиях обычно применяют полиномы не выше третьего порядка, так как полиномы более высоких степеней отражают случайные отклонения (что противоречит смыслу тенденции), а параметры a ₄ и т. д. экономически не интерпретируются.

Полином первой степени у_t = а ₀ + а ₁t на графике изображается прямой и используется для описания процессов, развивающихся во времени равномерно (рис. 2.1, а). В этом случае первые разности (абсолютные приросты) имеют приблизительно одинаковые значения.

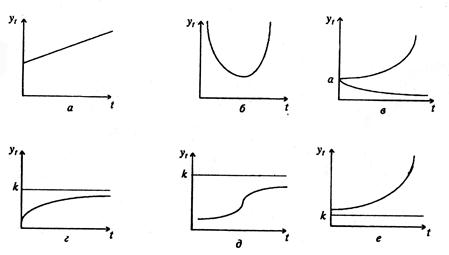
Рис. 2.1. Кривые роста:

а — полином 1-го порядка y_t = a₀ + a₁t; б — полином 2-го порядка y_t = a₀ + a₁t + a₂t²; в — экспонента у_t = аb^t; г — модифицированная экспонента у_t = k + аb^t; д — кривая Гомперца, если log а < 0; е — кривая Гомперца, если log а > 0, b > 1

Полином второй степени y_t = a₀ + a₁t + a₂t² можно применять в тех случаях, когда процесс развивается равноускоренно (рис. 2.1, б). На это указывает относительное постоянство вторых разностей.

Полином третьей степени y_t = a₀ + a₁t + a₂t² + a₃t³ применяют в том случае, если постоянны третьи разности.

Оценки параметров модели (2.3) определяются методом наименьших квадратов (МНK), суть которого состоит в нахождении таких параметров, при которых сумма квадратов отклонений расчетных значений уровней от фактических значений была бы минимальной, т. е. оценки параметров должны находиться в результате минимизации выражения

(2.4)

где n — длина временного ряда;

у_t — фактическое значение временного ряда;

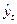— расчетное значение.

Система нормальных уравнений для определения параметров а _j уравнения (2.3) выглядит следующим образом:

(2.5)

где р — степень полинома.

Системы для оценки полиномов невысоких степеней выглядят намного проще. Нормальные уравнения для оценки параметров прямой приводятся к виду

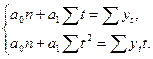(2.5,a)

Для параболы 2-го порядка система нормальных уравнений выглядит следующим образом:

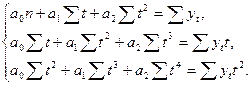(2.5,б)

Чтобы упростить систему (2.5), можно перенести начало координат в середину ряда. Тогда если до переноса начала координат t = 1, 2, 3, …, n, то после переноса для четного числа членов ряда t = …, -5, -3, -1, 1, 3, 5, …, для нечетного числа членов ряда t = …, -3, -2, -1,0, 1,2, 3,.... Система нормальных уравнений уменьшится, так как 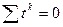, когда k — нечетное число.

В том случае, если переменная у_t изменяется с относительно постоянным темпом роста, для выравнивания целесообразно применять простую экспоненциальную (показательную) кривую

Y_t = ab ^t_,

где параметр а характеризует начальные условия развития, а параметр b — постоянный темп роста (рис. 2.1, в).

Если b > 1, то кривая растет вместе с ростом t и падает, если b < 1. Для оценки параметров а и b нужно сначала прологарифмировать выражение (2.6). В результате этого получим уравнение прямой:

log y_t = A + Bt,

Тогда система нормальных уравнений строится исходя из минимизации

Cледовательно, в нормальных уравнениях вместо фактических уровней выступают их логарифмы:

(2.7)

Однако при такой оценке параметров следует иметь в виду, что они (оценки) оказываются смещенными, так как в расчете участвуют не исходные уровни, а их логарифмы. Смещение будет тем значительнее, чем больше разность между последовательными уровнями временного ряда. Не приводит к смещению в подобных случаях нелинейный метод наименьших квадратов [22].

Более сложным вариантом экспоненциальной кривой является логарифмическая парабола

(2.8)

Прологарифмировав выражение (2.8), получим параболу

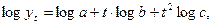
параметры которой можно также оценить с помощью метода наименьших квадратов.

Все рассмотренные типы кривых используются для описания монотонно возрастающих или убывающих процессов без насыщения.

Когда процесс характеризуется насыщением, т. е. имеется некоторое предельное значение в исследуемом явлении, то его следует описывать при помощи кривой, имеющей отличную от нуля асимптоту. Примером такой кривой может служить модифицированная экспонента

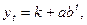(2.9)

Функция (2.9) имеет горизонтальную асимптоту у = k.

Если параметр а < 0, то асимптота будет находиться выше кривой, если а > 0, то ниже. При решении экономических задач чаще всего приходится иметь дело с кривой, у которой а < 0, b < 1. В этом случае рост уровней происходит с замедлением и стремится к некоторому пределу (рис. 2.1, г).

При решении экономических задач значение асимптоты можно определить исходя из свойств исследуемого процесса (например, коэффициент использования оборудования не может превышать 1). Иногда значение асимптоты задается экспертным путем. В этих случаях другие параметры кривой могут быть определены с помощью метода наименьших квадратов после приведения уравнения (2.9) к линейному виду:

(2.10)

где k — заданное значение асимптоты.

Прологарифмировав выражение (2.10), получим:

где параметры log. а и log b оцениваются исходя из системы нормальных уравнений (2.7). Для оценки параметров модифицированной экспоненты возможно применение как нелинейного метода наименьших квадратов, так и метода трех сумм или трех точек [22 ].

Итак, модифицированная экспонента хорошо описывает процессы, на развитие которых воздействует некоторый ограничивающий фактор, причем влияние этого воздействия растет вместе с ростом достигнутого уровня. Если воздействие ограничивающего фактора начинает сказываться только после определенного момента (точки перегиба), до которого процесс развивался по некоторому экспоненциальному закону, то для выравнивания используют S-образные кривые. Наибольшее применение эти кривые нашли в страховых и демографических расчетах. Самыми известными из S-образных кривых являются кривая Гомперца и логистическая кривая. Кривая Гомперца является несимметричной и имеет следующий вид:

Если log а < 0, кривая имеет S-образный вид и асимптота у = k проходит выше нее (рис. 2.1, д). Если 1оg а > 0, то асимптота y = k проходит ниже кривой, которая изменяется монотонно: при b < 1 монотонно убывает, при b > 1 монотонно возрастает (рис. 2.1, е). Наибольший интерес для решения экономических задач представляет вариант, когда log а < 0, b < 1 (см. рис. 2.1, д).

Если в модифицированной экспоненте вместо у_t ввести обратную величину, т. e. , то получим логистическую кривую

(2.12)

которую называют кривой Перла—Рида.

С помощью логистической функции (и ее различных форм) можно описать развитие нового производства. Сначала, когда технические методы недостаточно разработаны, издержки высоки и спрос на данный товар еще очень мал, производство развивается медленно. В дальнейшем, благодаря усовершенствованию методов изготовления, переходу к массовому производству и увеличению емкости рынка для данного товара, производство растет быстрее. Затем наступает период насыщения рынка, рост производства все более замедляется и, наконец, почти прекращается, т. е. наступает стабилизация производства на определенном уровне. Однако для коротких временных периодов выявленные закономерности следует обобщать с определенной осторожностью, так как на небольшом промежутке времени ряд может быть хорошо выравнен экспоненциальной кривой, хотя на самом деле это может оказаться первой половиной (до точки перегиба) логистической кривой.

Для оценки параметров модифицированной кривой, кривой Гомперца и логистической кривой можно применять упрощенные методы: метод трех сумм и метод трех точек [22].

Как уже отмечалось, проблема выбора формы кривой — одна из основных проблем, с которой сталкиваются при выравнивании ряда динамики. Ее решение во многом определяет результаты прогнозирования. Существует несколько практических подходов, облегчающих процесс выбора формы кривой роста.

1. Наиболее простой способ — визуальный, опирающийся на графическое изображение временного ряда. Подбирают такую кривую роста, форма которой подходит к описанию конкретного явления. Применение современных пакетов статистической обработки данных существенно облегчает работу исследователя.

2. Второй способ заключается в применении метода последовательных разностей, который помогает при выборе кривой полиномиального вида . Этот метод применим при условии, что уровни временного ряда могут быть представлены в виде суммы систематической составляющей Y_t и случайной компоненты E_t. Данный метод предполагает вычисление первых, вторых и т.д. разностей уровней ряда

Расчет ведется до тех пор, пока разности не будут примерно одинаковыми. Порядок разностей принимается за степень выравнивающего полинома.

3. Чаще всего на практике к выбору формы кривой подходят исходя из значения критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровней от расчетных, полученных выравниванием. Из рассматриваемых кривых выбирается та, которой соответствует минимальное значение критерия. Применение данного критерия дает практические результаты в том случае, если отбор функций проходит в два этапа:

— на первом происходит ограничение приемлемых функций исходя из содержательного анализа задачи;

— на втором осуществляется расчет критерия и выбор на его основе наиболее подходящей кривой роста.

Например, возможна ситуация, когда наилучшей функцией по данному критерию будет признана прямая, однако полученное на ее основе прогнозное значение будет отрицательным. Если из экономической сути показателя вытекает невозможность отрицательных значений (например, при прогнозировании объема выпускаемой продукции), то следует отказаться от функции прямой, выбрав менее „удачную” по данному критерию, но более соответствующую содержательному смыслу показателя. Более подходящей в этом случае может оказаться экспоненциальная кривая при b < 1 (см. рис. 2.1, в).

В современных пакетах статистической обработки данных и анализа временных рядов в качестве критерия выбирается средняя квадратическая ошибка

(2.13)

где у_t — фактическое значение ряда;

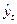— выравненное значение ряда;

n — длина ряда.

П р и м е р 2.3. Для определения тренда временного ряда, представленного в табл. 2.5 и на рис. 2.2, найдем параметры линейной, параболической и показательной функций, используя метод наименьших квадратов.

Т а б л и ц а 2.5

Квартал	1994 г	1995 г.	1996 г.	1997 г.	1998 г.	1999 г.
I	170,0	124,0	106,2	108,0	95,2	75,4
II	159,2	116,5	102,0	107,4	85,8	77,2
III	145,8	109,2	102,6	100,0	82,4	75,8
IV	126,4	108,0	109,2	101,6	74,0	83,4

Продажа мяса торгующими организациями, включая общественное питание, т

Рис 2.2 Динамика продажи мяса за 1994 — 1999 гг.

Для расчета параметров функций на основе МНК составляется система нормальных уравнений. Необходимые расчеты для вычисления коэффициентов представлены в табл. 2.6.

Система нормальных уравнений для линейной функции исходя из (2.5, а), примет вид

Решая эту систему, получим, что a ₀ = 146,86 и a ₁ = -3,26, т. е. уравнение прямой линии имеет вид

Аналогичные расчеты проводятся для параболы и показательной функции. В результате должны получиться следующие уравнения: для параболы —

для показательной функции —

Т а б л и ц а 2.6

Матрица определения параметров математических функций

Период	Условие обозначения времени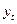
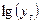
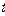
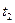
1994 г. I кв.					170,0	170,0	170,0	2,23	2,23
II кв.					159,2	318,4	1 273,6	2,20	4,40
III кв.					145,8	437,4	3 936,6	2,16	6,49
IV кв.					126,4	505,6	8 089,6	2,10	8,41
1995 г. I кв.					124,0	620,0	15 500,0	2,09	10,47
II кв.				1 296	116,5	699,0	25 164,0	2,07	12,40
III кв.				2 401	109,2	764,4	37 455,6	2,04	14,27
IV кв.				4 096	108,0	864,0	55 296,0	2,03	16,27
1996 г. I кв.				6 561	106,2	955,8	77 419,8	2,03	18,24
II кв.			1 000	10 000	102,0	1 020,0	102 000,0	2,01	20,09
III кв.			1 331	14 641	102,6	1 128,6	136 560,6	2,01	22,12
IV кв.			1 728	20 736	109,2	1 310,4	188 697,6	2,04	24,46
1997 г. I кв.			2 197	28 561	108,0	1 404,0	237 276,0	2,03	26,43
II кв.			2 744	38 416	107,4	1 503,6	294 705,6	2,03	28,43
III кв.			3 375	50 625	100,0	1 500,0	337 500,0	2,00	30,00
IV кв.			4 096	65 536	101,6	1 625,6	416 153,6	2,01	32,11
1998 г. I кв.			4 913	83 521	95,2	1 618,4	467 717,6	1,98	33,64
II кв.			5 832	104 976	85,8	1 544,4	500 385,6	1,93	34,80
III кв.			6 859	130 321	82,4	1 565,6	565 181,6	1,92	36,40
IV кв.			8 000	160 000	74,0	1 480,0	592 000,0	1,87	37,38
1999 г. I кв.			9 261	194 481	75,4	1 583,4	698 279,4	1,88	39,42
II кв.			10 648	234 256	77,2	1 698,4	822 025,6	1,89	41,53
III кв.			12 167	279 841	75,8	1 734,4	922 258,6	1,88	43,23
IV кв.			13 824	331 776	83,4	2 001,6	1 152 921,6	1,92	46,11
Итого:		4 900	90 000	1 763 020	2 545,3	28 062,0	7 657 969,0	48,35	589,33

На основе полученных уравнений определяются теоретические уровни тренда для каждого периода анализируемого ряда динамики. Так, для прямой они составят:

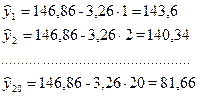
Аналогичные расчеты проводятся для параболы и для показательной функции. Результаты расчетов приведены в табл. 2.7.

По итоговым данным этой таблицы определяем по формуле (2.11) средние квадратические ошибки:

для прямой —

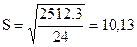
для параболы —

для показательной функции —

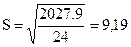
Из сравнения полученных значений следует, что предпочтение в выборе функции следует отдать параболе

т. е. при построении точечных и интервальных прогнозов будет использоваться полученное уравнение.

Дата добавления: 2014-01-06