Гармонический анализ

Во многих случаях сглаживание временных рядов с помощью кривых роста не дает удовлетворительных результатов, так как в остатках наблюдается автокорреляция (см. п. 3.2). С другой стороны, в рядах динамики нередко содержатся заметные периодические колебания, которые нельзя описать с помощью кривых роста. В таких случаях на практике можно прибегнуть к гармоническому анализу, суть которого состоит в том, что исходный ряд Y_t преобразовывается в новый Y_k(t):

Т а б л и ц а 2.7

Матрица определения средней квадратической ошибки

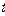
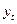
Период			Теоретические уровни по моделям	Отклонение фактических уровней от 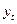теоретических значений
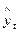
прямая	показательная функция	парабола	прямолинейная функция	показательная функция	парабола 2-го порядка
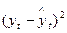
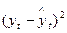
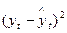
1994 г. I кв.		170,0	143,6	146,1	155,2	697,1	571,5	217,9
II кв.		159,2	140,4	141,8	148,9	356,0	303,9	105,3
III кв.		145,8	137,1	137,6	142,9	76,3	67,7	8,3
IV кв.		126,4	133,8	133,5	137,2	54,8	50,3	115,8
1995 г. I кв.		124,0	130,5	129,5	131,7	42,8	30,7	59,1
II кв.		116,5	127,3	125,7	126,5	116,1	84,7	99,8
III кв.		109,2	124,0	122,0	121,6	219,3	163,4	153,0
IV кв.		108,0	120,7	118,4	116,9	162,4	107,5	79,7
1996 г. I кв.		106,2	117,5	114,9	112,6	127,2	75,1	40,4
II кв.		102,0	114,2	111,5	108,5	149,2	89,6	41,8
III кв.		102,6	111,0	108,2	104,6	69,7	30,9	4,2
IV кв.		109,2	107,7	105,0	101,1	2,3	18,0	65,5
1997 г. I кв.		108,0	104,4	101,9	97,8	12,8	37,8	103,2
II кв.		107,4	101,2	98,8	94,9	39,0	73,4	157,4
III кв.		100,0	97,9	95,9	92,1	4,4	16,7	61,8
IV кв.		101,6	94,6	93,1	89,7	48,6	72,8	141,5
1998 г. I кв.		95,2	91,4	90,5	87,5	14,7	23,9	58,6
II кв.		85,8	88,1	87,6	85,7	5,3	3,4
III кв.		82,4	84,8	85,0	84,1	5,9	7,0	2,7
IV кв.		74,0	81,6	82,5	82,7	57,3	72,6	76,0
1999 г. I кв.		75,4	78,3	80,1	81,7	8,4	21,9	39,2
II кв.		77,2	75,0	77,7	80,9	4,7	0,3	13,6
III кв.		75,8	71,8	75,4	80,4	16,2	0,2	21,0
IV кв.		83,4	68,5	73,2	80,2	221,7	104,6	10,5
Итого:		2 545,3	2 545,4	2 535,7	2 545,4	2 512,2	2 027,9	1 676,3

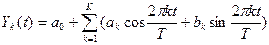
где a ₀, a _k, b_k — неизвестные параметры Фурье, которые находятся по методу наименьших квадратов;

k — гармоника ряда, которая чаще всего берется от 1 до 4

(k<);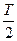

Т — период колебаний.

Частным случаем гармонического анализа является описание сезонной компоненты, когда период колебания Т равен 12 месяцам. Для изучения сезонности ряд динамики исследуемого годового явления в радиальной системе лучше представить следующим образом:

t

11-

Рад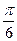

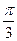
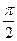
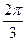
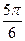
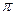
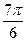
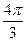
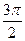
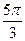
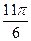
Уровни

y1

y2

y3

y4

y5

y6

y7

y8

y9

y10

y11

y12

В этом случае исходный ряд Y_t будет аппроксимироваться функцией

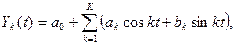(2.12)

коэффициенты Фурье a ₀, a _k, b_k определятся из следующих отношений:

.

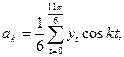
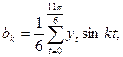
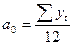Наиболее подходящей считается та функция Y_k(t), при которой средняя квадратическая ошибка

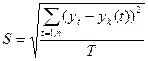(2.13)

имеет наименьшее значение.

Значения cos kt и sin kt при k, равном 1, 2, 3, 4, находим по табл. 1 (прил. 1). Тогда первая гармоника при Т = 12 будет выглядеть следующим образом:

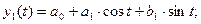(2.14)

где

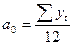; (2.15)

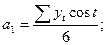(2.16)

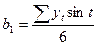. (2.17)

Ряд Фурье с двумя гармониками имеет вид

,

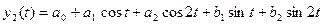где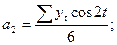

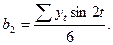
После выделения из исследуемого ряда систематической составляющей (тренда) и периодической составляющей (если она присутствует) переходят к анализу случайной компоненты.

Пример 2.4. Проиллюстрируем построение модели внутригодовой динамики по первой гармонике ряда Фурье (2.14).

Т а б л и ц а 2.8

Месяц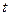
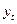
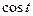
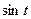
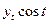
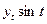
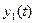
Январь		36,700	1,000		36,700		39,536
Февраль		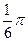37,400	0,866	0,500	32,389	18,700	38,934
Март		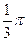40,600	0,500	0,866	20,300	35,161	38,597
Апрель		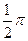39,500				39,500	38,616
Май		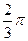38,600	-0,500	0,866	-19,300	33,429	38,986
Июнь		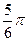39,400	-0,866	0,500	-34,121	19,700	39,607
Июль		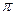39,500	-1,000		-39,500		40,314
Август		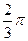41,400	-0,866	-0,500	-35,853	-20,700	40,916
Сентябрь		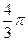40,800	-0,500	-0,866	-20,400	-35,334	41,253
Октябрь		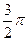41,700		-1,000		-41,700	41,234
Ноябрь		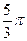40,600	0,500	-0,866	20,300	-35,161	40,864
Декабрь		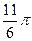42,900	0,866	-0,500	37,152	-21,450	40,243
Итого:	479,100	-	-	-2,333	-7,855	479,100

Коэффициенты Фурье для первой гармоники определяются по формулам (2.15 — 2.17):

; .

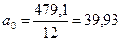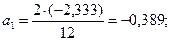
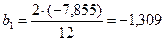Тогда первая гармоника ряда имеет вид

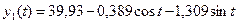
На основе полученного уравнения определяются расчетные значения для каждого месяца (табл. 2.8, графа 8).

………………………………………………………………

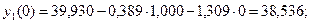
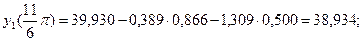
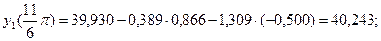
Подобным образом можно построить вторую, третью и т. д. гармоники, а затем по формуле (2.13) вычислить средние квадратические ошибки и по минимальному значению определить наилучшую гармонику.

Дата добавления: 2014-01-06