Прогнозирование явлений с помощью индексов сезонности

Определив влияние сезонного фактора, можно использовать най­денные закономерности для прогнозирования дальнейшего развития изучаемого явления. Определив все три компоненты временного ряда, можно попытаться использовать найденные закономерности в перспективе. При этом можно оценить значения параметров тренда и краткосрочных сезонных колебаний. Случайные колеба­ния можно оценить вероятностным путем. При экстраполяции сле­дует учитывать, что чем продолжительнее период предсказания, тем вероятнее сделать большую ошибку. Поэтому следует по мере получения новых фактических данных пересматривать модели.

В общем виде модель прогноза с помощью индексов сезонности на любой месяц (квартал) можно представить следующим образом:

,

где — прогнозируемое значение показателя в момент

времен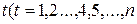и или );

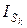— индекс сезонности (или средний индекс сезонности по расположению) -го месяца или -квартала (= 1, 2, 3, 4 либо = 1, 2,..., 12);

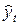— оценка исследуемого показателя, вычисленная по урав­нению тренда.

Так как случайную величину определить точно нельзя, то можно с определенной вероятностью утверждать, что вычисленные по модели (6.4) прогнозные оценки будут отличаться от истинной на величину

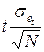
где 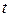— число, показывающее, во сколько раз отличается средняя величина от своего отклонения при определенной вероятности;

— среднее квадратическое отклонение случайной вели-чины ;

— число одноименных периодов.

Пример 6.2. По данным о продаже яиц в магазинах города по месяцам за три года вычислим индексы сезонных колебаний реализации яиц (табл. 6.3).

Таблица 6.3

Среднедневная реализация яиц, тыс.шт.

месяц		Показатели сезонности
1998 г.	1999 г.	2000 г.		мультиплика- тивные, %	адитивные
Январь	94,2	98,8	91,0	94,7	94,8	-5,01
Февраль	95,1	99,4	92,4	95,6	95,8	-4,2
Март	96,7	99,5	100,3	98,8	99,0	-1,0
Апрель	97,6	101,4	99,5	99,5	99,7	-0,3
Май	90,1	89,2	93,1	90,8	91,0	-9,0
Июнь	118,7	124,4	125,9	123,0	123,2	23,2
Июль	116,8	108,4	116,7	114,0	114,2	14,2
Август	100,1	91,0	98,5	96,5	96,7	-3,3
Сентябрь	101,5	101,9	94,8	99,4	99,6	-0,4
Октябрь	92,5	94,2	96,3	94,3	94,5	-5,5
Ноябрь	88,9	89,8	92,2	90,3	90,5	-9,5
Декабрь	99,1	100,0	103,1	100,7	100,9	0,9
Средний уровень	99,3	99,8	100,3	99,8	100,0

Рассматривая средние уровни ряда за каждый год, видим, что ряд имеет незначительную тенденцию к росту, поэтому индексы сезонности будем вычислять без предварительного выравнивания.

1. По данным табл. 6.3 вычислим усредненные значения уров­ней по одноименным периодам способом средней арифметической (см. графу 5):

январь: (94,2 + 98,8 + 91,0): 3 = 94,7 и т. д.

2. Затем по вычисленным помесячным средним уровням 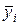или по среднегодовым уровням определим общий средний уровень ряда:

.

3. Далее рассчитаем для каждого месяца индексы сезонности (см. графу 6):

январь: 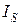= 94,7: 99,8 = 0,948 (94,8 %) и т. д.

Совокупность вычисленных индексов характеризует волну про­дажи во внутригодовой динамике. Полученные данные можно изо­бразить в виде линейной диаграммы (рис. 6.1).

Р и с. 6.1. Сезонная волна реализации яиц по месяцам за три года

Из табл. 6.3 (см. графу 6) и графика видно, что сезонные колебания характеризуются повышением в июне (+23,2 %), июле (+14,2 %) и декабре (+0,9 %) и снижением в других месяцах.

Пример 6.3. Рассмотрим временной ряд, имеющий тенден­цию развития (табл. 6.4).

Таблица 6.4

Реализация молочной продукции в регионе

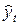
Год	Квартал			Показатели сезонности, %
	I	54,6	62,4	87,5
	II	80,6	65,2	123,6
	III	78,8	67,9	115,97
	IV	53,5	70,7	75,6
	I	53,2	73,6	72,3
	II	97,5	76,4	127,6
	III	98,7	79,2	124,6
	IV	60,5	81,9	73,8

	I	56,4	84,8	66,5
	II	112,1	87,6	128,0
	III	114,5	90,3	126,7
	IV	74,6	93,2	80,1
	I	66,6	96,0	69,4
	II	126,6	98,8	128,1
	III	132,8	101,5	130,7
	IV	76,7	104,4	73,5

Произведем следующие действия.

1. Для определения индексов сезонности сначала нужно найти уравнение тренда, наилучшим образом отображающее динамику развития исследуемого процесса (рис. 6.2). Наилучшим образом исследуемое явление отображает уравнение прямой линии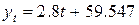

Рис. 6.2. Реализация молочной продукции в регионе

В табл. 6.4 (см. графу 4) приведены уровни, сглаженные по уравнению тренда.

2. Для каждого квартала определяются показатели сезонности
как отношение фактических уровней к выравненным по уравне­нию тренда (см. табл. 6.4, графу 5).

3. Индексы сезонности рассчитываются как среднее арифмети­ческое показателей сезонности, взятых по одноименным пе­риодам:

I квартал: и т.д.(табл. 6.5).

Таблица 6.5

Индексы сезонности

Квартал	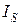,%	Выравненные индексы
I	73,93	73,71
II	126,83	126,45
III	124,52	124,14
IV	75,76	75,53

4. Для проверки правильности вычислений индексов вычисля­ется средний индекс сезонности:

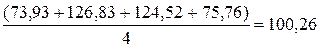
Если средний из индексов отличается от 100 %, то следует произвести их выравнивание путем умножения на величину, об­ратную среднему индексу сезонности.

5. Для нахождения уровней ряда, в которых элиминировано влияние сезонности, необходимо фактические уровни поделить на соответствующий выравненный индекс.

Выравненные индексы сезонности (см. табл. 6.5) составляют модель сезонной волны реализации молочной продукции во внутригодовом цикле. Наибольший объем продаж приходится на II и III кварталы с превышением среднегодового уровня соответственно на 26,6 и 24,4%. В I и IV кварталах происходит снижение сред­негодового уровня соответственно на 26,2 и

24,5 %.

На основе полученных индексов сезонности можно построить уравнения прогноза для соответствующих кварталов:

для I квартала;

для II квартала;

для III квартала;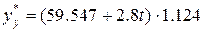

для IV квартала.

6.4. МОДЕЛИРОВАНИЕ СЕЗОННЫХ КОЛЕБАНИЙ

При исследовании периодических явлений и их описании це­лесообразно использовать модели сезонных колебаний, которые

строятся при помощи гармонического анализа (см. п. 2.2.3). Расчет для построения модели можно провести по следующей схеме.

1. На первом этапе выделяется общая тенденция и оцениваются параметры уравнения тренда. Правильность определения тренда является обязательным условием сезонного компонента.

2. На втором этапе устанавливается тип связи между компо­нентами ряда (аддитивная или мультипликативная). В зависимости от этого сезонные колебания выражаются в различных показате­лях. В случае аддитивной связи сезонные колебания рассчитыва­ются в абсолютных величинах, а при мультипликативной — в от­носительных (%). Поэтому прежде чем приступить к расчету се­зонных колебаний, необходимо установить вид связи сезонной и
трендовой компонент.

Тип связи можно определить по динамике отклонений факти­ческих уровней от тренда:

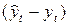
или

Если абсолютные отклонения имеют тенденцию к росту, а отно­сительные варьируют приблизительно на одном уровне, то это свидетельствует о мультипликативной связи тренда и сезонной компоненты [9 ].

Тип связи можно определить и по нормальному распределению отклонений фактических уровней от тренда. Если абсолютные сезонные отклонения распределяются по нормальной кривой, то связь между компонентами ряда аддитивна, если же по нормальной кривой распределяются относительные отклонения, то связь между компонентами мультипликативна.

3. Далее необходимо описать сезонные колебания. Выравнивание ряда, имеющего периодическую составляющую, можно производить при помощи гармонического анализа, суть которого состоит в том, что исходный ряд преобразуется в новый 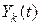, где роль периодической составляющей вычерчивается особенно ярко. Выявление сезонной компоненты является частным случаем гармонического анализа, при котором период колеба­ния Т равен 12 месяцам (см. п. 2.2.3). Если имеются данные больше чем за 12 месяцев, например за 24 или 36 (т. е. за 2 или 3 года), то для выравнивания гармониками лучше брать период в 12 месяцев (или поквартально), предшествующих предсказываемому периоду.

Выравнивание по ряду Фурье дает хорошие результаты как в рядах динамики, содержащих сезонную компоненту, так и при анализе отклонений фактических уровней от теоретических, полученных по уравнению тренда.

5. Если предположить, что в будущем периоде сохранится эта же амплитуда колебаний, то можно попытаться оценить значение исследуемого показателя в перспективе. Однако при расчете значений функции следует исходить из значений предполагаемого тренда, а не от среднего уровня . В общем виде модель развития того или иного социально-экономического явления исходя из взаимосвязи компонент можно записать так:

Или

где 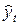— уравнение тренда;

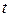— номер наблюдения (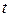= 1, 2, 3,..., Т);

— номер гармоники;

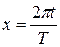
Таким образом, если необходима простая характеристика се­зонной волны, достаточно вычислить индексы сезонности указан­ными выше способами. Если же речь идет о методах выявления сезонного компонента, то для этого целесообразно:

1) определить тренд рассматриваемого временного ряда;

2) выявить вид связи между трендом и сезонной компонентой;

3) произвести выравнивание исходных данных по ряду Фурье;

4) оценить значимость полученной модели (для этого нужно проанализировать отклонения рассматриваемого ряда от получен­ных теоретических значений).

7. АДАПТИВНЫЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ

7.1. СУЩНОСТЬ АДАПТИВНЫХ МЕТОДОВ

В настоящее время одним из наиболее перспективных направлений в прогнозировании временных рядов являются адаптивные методы. Считается, что характерная черта этих методов — их способность непрерывно учитывать эволюцию динамических ха­рактеристик изучаемых процессов, „подстраиваться" под эту эво­люцию, придавая тем больший вес и тем более высокую инфор­мативную ценность имеющимся наблюдениям, чем ближе они к текущему моменту прогнозирования. Все это делает эффективным
их применение для прогнозирования неустойчивых рядов с изме­няющейся тенденцией.

Оценивание коэффициентов адаптивной модели обычно осуще­ствляется на основе рекуррентного метода, который отличается от метода наименьших квадратов и других методов тем, что не требует повторения.всего объема вычислений при появлении новых данных.

Сущность адаптивных методов заключается в возможности по­строения корректирующихся моделей, способных учитывать ре­зультат прогноза, сделанного на предыдущем шаге. Быстроту ре­акции модели на изменение в динамике процесса характеризует так называемый параметр адаптации (в некоторых учебниках Он называется параметром сглаживания или дисконтирования). Этот параметр должен быть выбран таким образом, чтобы обеспечива­лось адекватное отображение тенденции при одновременной филь­трации случайных отклонений. В качестве критерия оптимально­сти при выборе параметра адаптации обычно принимают критерий минимума среднего квадрата ошибок прогнозирования [14, 21].

Наиболее простым из многочисленного класса адаптивных методов является метод экспоненциального сглаживания (метод Брауна).

7.2. МЕТОД ЭКСПОНЕНЦИАЛЬНОГО СГЛАЖИВАНИЯ

Сущность метода экспоненциального сглаживания заключается в том, что временной ряд сглаживается с помощью взвешенной скользящей средней, в которой веса подчиняются экспоненциаль­ному закону, по которому более ранним наблюдениям придается меньший вес, чем более поздним.

Если предполагается, что некоторый процесс может быть описан полиномом степени р, т. е.

,

то коэффициенты предсказывающего полинома

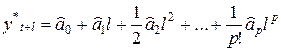(7.1)

могут быть вычислены через экспоненциальные средние соответ­ствующих порядков.

Экспоненциальной средней 1-го порядка ряда называется выражение

,

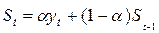где — значение экспоненциальной средней в момент времени ;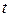

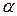— параметр сглаживания (адаптации),

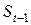— значение экспоненциальной средней в момент времени .

Брауном выведена следующая рекуррентная формула для определения экспоненциальной средней -го порядка в точке :

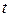(7.2)

На практике обычно используются полиномы не выше 2-го порядка. Формулы, необходимые для расчета, приведены в табл. 7.1.

При построении прогнозов с помощью метода экспоненциаль­ного сглаживания одной из основных проблем является выбор оп­тимального параметра сглаживания а. Если он близок к единице, то при прогнозе учитывается в основном влияние лишь последних наблюдений, если он близок к нулю, то веса, по которым взве­шиваются уровни временного ряда, убывают медленно и при про­гнозе в значительной степени учитываются все прошлые наблю­дения.

Таблица 7.1

Основные формулы для прогнозирования с помощью метода экспоненциального сглаживания

Вид модели	Начальные условия	Экспоненциальные средние	Оценка коэффициентов	Модель прогноза	Ошибка прогноза
Постоянная
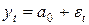
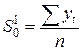
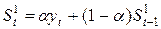
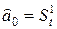
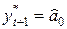
Линейная
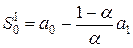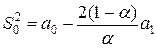
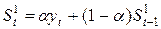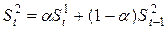
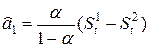
Квадратичная

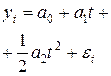
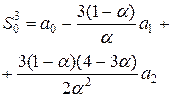
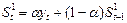
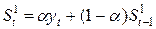
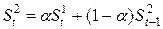
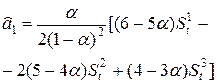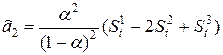
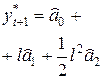
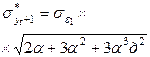
Точного метода выбора оптимальной величины параметра 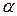нет. В отдельных случаях предлагается определить ее по формуле:

, (7.3)

где 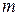- число наблюдений, входящих в интервал сглаживания.

Как отмечалось выше, в качестве критерия оптимальности при выборе параметра адаптации можно использовать критерий минимума среднего квадрата ошибок прогнозирования.

В том случае, если процесс подвержен внезапным изменениям, необходимо изменениям, необходимо выявить момент их возникновения, модифицировать параметры надлежащим образом и на необходимое время. Для этого можно использовать так называемый трэкинг-сигнал (следящий сигнал), который улавливает момент, когда необходимо вмешательство исследователя. Формула трэкинг-сигнала имеет следующий вид:

, (7.4)

где 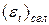- сглаженная ошибка, вычисляемая по формуле

;

- абсолютные значения ошибки прогноза, получаемые из следующего выражения:

,

где - параметр сглаживания.

Для которых временных рядов предлагается за начальное значение сглаженной ошибки выбирать ноль, а за начальное значение модуля сглаженной ошибки 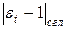- первое значение модуля ошибки [21].

Схема прогнозирования временных рядов по методу экспоненциального сглаживания с использованием трэкинг-сигнала состоит из следующих этапов.

1. Выбирают вид модели экспоненциального сглаживания.

2. Параметр 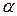определяется по формуле (7.3) либо задается исследователем.

3. Задают начальные условия.

4. Вычисляют начальные условия.

5. Находят экспоненциальные средние.

6. Определяют оценки коэффициентов модели прогноза.

7. Осуществляют прогноз на одну точку вперед.

8. Находят отклонения фактического значения временного ряда от прогнозируемого.

9. Рассчитывают величину трэкинг-сигнала, которая сравнива­ется с пороговым значением с учетом выбранной вероятности [21 ].

10. а) если трэкинг-сигнал не выходит за пороговое значение, то переходят к 5-му этапу схемы прогнозирования;

б) если трэкинг-сигнал выходит за пороговое значение, то па­раметр 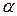увеличивают на какую-либо величину и переходят к 5-му этапу, производя расчеты с новым параметром а для периода (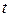+ 2).

Такая последовательность осуществляется до тех пор, пока не будет проанализирован весь временной ряд. Если для последнего уровня ряда величина трэкинг-сигнала не выходит за пороговые значения, то вычисляют оценки параметров прогноза и осуществляют прогноз на заданный период упреждения. Если трэкинг-сигнал выходит за пороговое значение, то параметр у следует увеличить на какую-либо величину, а затем перейти к этапам 2,4 — 10. В том случае, если применение трэкинг-сигнала не нужно, а прогноз осуществляется по методу простого экспоненциального сглаживания, схема повторяется до 9-го этапа (кроме 3), а затем переходят к 5-му этапу и т. д. до последнего уровня ряда. Прогноз осуществляется по формуле (7.1) путем подстановки в нее последних значений коэффициентов и времени упреждения.

Пример 7.1. В качестве примера для иллюстрации применения метода экспоненциального сглаживания рассмотрим времен­ной ряд продаж мяса торгующими организациями (см. пример 2.3). Тренд этого ряда можно описать параболой

Для построения модели прогноза использовались формулы, взя­тые из табл. 7.1 для квадратичной модели. В наших расчетах использовалась величина параметра сглаживания 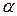= 0,4, которую получили с помощью критерия минимума средней квадратической ошибки. Прогноз продаж осуществлялся на период с I по IV квар­тал 2000 года. Расчет производился по формуле (7.1), где 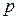= 2.

Как видно из табл. 7.1, для определения оценок коэффициен­тов ,и 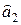помимо значения а необходимо найти экспоненциальные средние , , 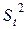.Для их расчета использовалась ре­куррентная формула (7.2). Сначала были определены начальные условия

; ; ,

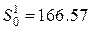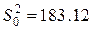Таблица 7.2

Прогнозирование по методу экспоненциального сглаживания

Период	Экспоненциальные средние	Оценки коэффициентов модели прогноза
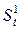
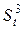
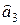
1994 г. I	167,9	177,0	181,3	154,0	-1,76	-2,15	170,0	-
II	164,4	172,0	177,6	154,9	-1,05	-0,88	159,2	151,2
III	157,0	166,0	173,0	145,9	-1,19	-0,91	145,8	153,4
IV	144,8	157,5	166,8	128,5	-1,80	-1,55	126,4	144,3
1995 г. I	136,5	149,1	159,7	121,8	-1,50	-0,90	124,0	126,0
II	128,5	140,8	152,2	115,1	-1,28	-0,47	116,5	119,9
III	120,8	132,8	144,4	108,3	-1,13	-0,19	109,2	113,5
IV	115,7	125,9	137,0	106,2	-0,73	0,35	108,0	107,1
1996 г. I	111,9	120,3	130,3	105,0	-0,41	0,70	106,2	105,6
II	107,9	115,4	124,4	102,0	-0,33	0,69	102,0	105,0
III	105,8	111,5	119,2	102,0	-0,10	0,87	102,6	102,1
IV	107,2	109,8	115,4	107,6	0,39	1,35	109,2	102,3
1997 г. I	107,5	108,9	112,8	108,7	0,40	1,14	108,0	108,6
II	107,5	108,3	111,0	108,5	0,30	0,83	107,4	109,7
III	104,5	106,8	109,3	102,4	-0,15	0,11	100,0	109,2
IV	103,3	105,4	107,7	101,5	-0,12	0,13	101,6	102,3
1998 г. I	100,1	103,3	106,0	96,4	-0,38	-0,22	95,2	101,5
II	94,4	99,7	103,5	87,4	-0,78	-0,71	85,8	95,9
III	89,6	95,7	100,3	82,1	-0,81	-0,62	82,4	86,3
IV	94,9	95,4	98,8	97,1	0,48	1,13	74,0	81,0
1999 I	87,1	92,1	95,8	81,0	-0,67	-0,52	75,4	98,1
II	83,2	88,5	92,9	76,9	-0,65	-0,42	77,2	80,1
III	91,9	89,9	91,7	97,8	0,95	1,71	75,8	76,0
IV	88,5	89,3	90,7	88,3	0,05	0,27	83,4	99,6

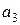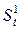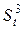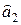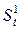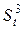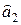где за , , взяты оценки параболического тренда. Затем были рассчитаны ,и , ,,и осуществлен прогноз на II квартал 1994 года. Далее по рекуррентной формуле (7.2) вычислялись новые ,,, а по ним определялись соответствующие ,и для построения прогноза на III квартал 1994 года и т. д. В табл. 7.2 представлен процесс построения модели прогноза по методу экспоненциального сглаживания. При прогнозировании продажи мяса использовались величины экспоненциальных сред­них 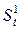,и 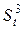, равные 88,5,89,3 и 90,7 соответственно, и коэффициенты модели прогноза ,и 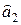равные соответственно 88,3, 0,05 и 0,27.

В табл. 7.3 представлены результаты прогноза продаж и его ошибки на I — IV кварталы 2000 года, а также доверительные интервалы для 5% уровня значимости.

Таблица 7.3

Прогноз продажи мяса торгующими организациями на 2000 год, т

Квартал	Прогноз продажи	Ошибка прогноза в абсолютном выражнии	Доверительный интервал
Нижняя граница	Верхняя граница
I	88,5	9,6	74,6	93,8
II	88,6	12,5	73,9	98,9
III	88,7	15,5	73,0	104,1
IV	88,9	18,6	72,1	109,3

7.3. АДАПТИВНЫЕ МЕТОДЫ СЕЗОННЫХ КОЛЕБАНИЙ

В том случае, если временные ряды содержат периодическую компоненту, можно использовать адаптивные модели с мульти­пликативными (7.5) и аддитивными (7.6) коэффициентами сезонности:

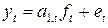; (7.5)

(7.6)

где динамика величины 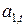характеризует тенденцию развития процесса;

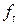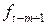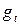, ,…,— мультипликативные коэффициенты се­зонности;

, , …, — аддитивные коэффициенты сезонности;

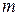— количество фаз в полном сезонном цикле (т = 4 или 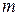- 12);

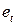— случайная компонента с нулевым математическим ожи­данием.

Выбор той или иной модели будет продиктован характером динамики исследуемого процесса (см. п. 6.4). Модель Хольта — Уинтерса (7.5) объединяет, мультипликативно линейный рост и сезонный эффект. Прогноз по этой модели на 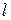шагов вперед определяется выражением

, 1< m

Обновление коэффициентов осуществляется следующим образом:

;

;

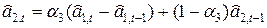
В качестве коэффициента сезонности берется его наиболее поздняя оценка. Если временной ряд содержит только сезонные колебания, то из уравнения прогноза и формул исключается оценка тренда .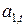

Прогноз по модели Тейла — Вейджа (7.6) определяется выражением

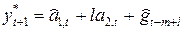
Коэффициенты обновляются следующим образом:

;

;

.

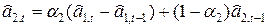Оптимальные значения параметров адаптации можно определять экспериментальным путем, взяв за критерий оптимальности минимум стандартного отклонения ошибки [14].

Дата добавления: 2014-01-06