Простая корреляция и регрессия рядов динамики

КОРРЕЛЯЦИЯ И РЕГРЕССИЯ РЯДОВ ДИНАМИКИ

Общественные явления находятся в постоянном развитии. Изменения одного явления часто вызывают изменения другого или нескольких других, т. с. явления в некоторой степени взаимосвязаны между собой. Наиболее общим видом связи между процессами служит стохастическая связь, которая проявляется в том, что существуют общие случайные факторы, влияющие на каждое явление неодинаково. Например, стохастически зависимыми можно считать объем произведенной продукции и коэффициент ис­пользования рабочего времени на предприятий, так как оба по­казателя зависят от квалификации персонала, ритмичности снаб­жения и др.

Частным случаем стохастической связи является корреляционная связь, при которой одному значению одного явления соответствует множество значений другого. Целью корреляционного анализа является исследование тесноты связи между явлениями.

Говоря о корреляционном анализе, нельзя забывать о регрес­сионном, целью которого является анализ формы связи. Резуль­таты такого анализа приобретают количественное выражение в уравнениях и коэффициентах регрессии.

Корреляционному и регрессионному анализу должен предшествовать всесторонний теоретический анализ возможности существования связи между явлениями. А так как методы корреляционного анализа предъявляют ряд требований к временным рядам, то предварительно необходимо выяснить, удовлетворяют ли уровни исследуемых рядов свойствам случайности, независимости и нормальности. Наиболее важным из них является требование о слу­чайности (об отсутствии тенденции).

Простой корреляцией принято называть корреляцию между' двумя факторами. Для определения тесноты связи между двумя явлениями обычно применяют индекс корреляции:

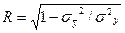
(8.1)

где Оу — средний квадрат отклонений фактических значений ре­зультативного признака от теоретических, рассчитанных по урав­нению регрессии;

-дисперсия результатов признака

Абсолютное значение индекса корреляции находится в пределах

О < 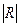< 1.

Если R= 0, то явления между собой не связаны, если R = 1, то считается, что между явлениями существует функциональная связь. Считается, что чем ближе значение индекса корреляции к единице, тем теснее связь между явлениями.

Индекс корреляции (8.1) пригоден для оценки тесноты связи при любой форме парной связи. Если же известно, что связь между явлениями линейна, то можно пользоваться коэффициентом корреляции, определенным по способу моментов:

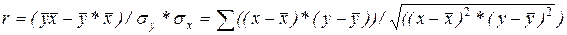(8.2)

Также можно использовать модифицированный коэффициент кор­реляции (1.11).

Линейный коэффициент корреляции, так же как и индекс кор­реляции, может принимать значения в интервале -1 < r < 1. Отрицательное значение коэффициента корреляции указывает на обратную связь между явлениями.

При оценке тесноты связи между факторами, уровни которых представлены в динамике, необходимо учитывать такое явление, как автокорреляция в наблюдениях, т. е. зависимость между уров­нями одного и того же временного ряда. Для того чтобы получить правильную картину связи между временными рядами, не иска­женную автокорреляцией, необходимо из каждого ряда исключить основную тенденцию и найти корреляцию отклонений от тренда по следующей формуле:

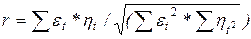(8.3)

где ε _t, η_t — отклонения от соответствующих тенденций исследу­емых явлений.

Вторая особенность применения корреляционного анализа к ря­дам динамики состоит в возможном наличии временного лага, т. е. когда влияние одного явления на другое осуществляется с некоторым запаздыванием (например, капитальные вложения ока­зывают влияние на изменение объема продукции через опреде­ленный период). Величину этого запаздывания (лага) можно определить на основе конкретного анализа данных и вычислить по коэффициентам корреляции (1.11). Наличие пиков в функ­ции r(t) указывает на присутствие временного лага, а его длина соответствует г периодам.

Третьей особенностью корреляции временных рядов является возможность переменной корреляции, которая показывает, как ме­няется значение коэффициента корреляции с течением времени. По серии коэффициентов корреляции, вычисленных в скользящем порядке с вычитанием одного уровня ряда и прибавлением сле­дующего через определенный интервал скольжения, можно полу­чить более полные сведения о том, как изменялась теснота связи во времени.

При определении формы связи между экономическими времен­ными рядами наиболее часто пользуются следующими функциями:

прямая линия —

_Yх = а₀ + а₁ х; (8.4)

парабола —

(8.5)

_Yх = а₀ + а₁ х; + а₂х;

гипербола —

(8.6)

_Yх = а₀₊ а_1/ х;

показательная функция—

(8.7)

_Yх = а_0*а₁^x

степенная функция —

(8.8)

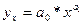
Параметры функций (8.4) — (8.9) обычно определяются ме­тодом наименьших квадратов. Система нормальных уравнений ана­логична системе (2.5). При определении параметров вместо пока­зателя ґ в уравнениях (2.5) используются значения показателя x. В том случае, если в ряду остатков от регрессионной модели Y_x наблюдается автокорреляция, а явления Y_t и X_t развиваются по одинаковым тенденциям, можно линейно ввести в уравнение регрессии фактор времени t. Это позволит устранить или хотя бы уменьшить автокорреляцию в наблюдениях.

Дата добавления: 2014-01-06