Решение задачи отыскания максимума линейной функции

Симплексный метод

Метод применяется для решения задачи линейного программирования, записанной в канонической форме.

На первом шаге решения симплексным методом все переменные нужно разделить на 2 группы (основные, или базисные, и неосновные). В качестве основных переменных можно выбрать такие m переменных, каждая из которых входит только в одно из m уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных. Например, если число дополнительных переменных равно числу уравнений, то этому правилу удовлетворяют дополнительные переменные. Если они имеют те же знаки, что и соответствующие им свободные члены в правых частях уравнений, то полученное базисное решение будет допустимым.

Симплексный метод состоит в упорядоченном переходе от одного допустимого базисного решения к другому, при этом значение целевой функции не должно становиться хуже (относительно цели). Геометрический смысл метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой линейная функция принимает лучшее (или по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение (если задача имеет конечный оптимум) или не будет установлено, что задача не имеет оптимума или он бесконечен.

Сформулируем критерии оптимальности найденных решений для задач на поиск максимума и задач на поиск минимума целевой функции.

1. Если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то найденное решение задачи отыскания максимума линейной функции является оптимальным.

2. Если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то найденное решение задачи отыскания минимума линейной функции является оптимальным.

Рассмотрим примеры применения симплексного метода.

Пример 2. Для изготовления двух видов продукции Р₁ и Р₂ используют 4 вида ресурсов R₁, R₂, R₃ и R₄. Составить такой план производства продукции (х₁ и х₂), при котором прибыль от ее реализации будет максимальной при условии, что потребление ресурсов по каждому виду ресурсов ограничено имеющимися запасами b_i (i=1,2,3,4). Цена реализации единицы продукции Р₁ и Р₂ равна c₁ =5 и c₂ =3. Запасы ресурсов, число единиц ресурсов a_ij, затрачиваемых на изготовление единицы продукции, приведены в таблице 2.1.

Таблица 2.1. Исходные данные

Вид ресурса	Запас ресурса	Число ед. ресурсов на ед. продукции
Р1	Р2
R1	b1 =15	a11= 2	a12= 3
R2	b2 =12	a21= 1	a22= 2
R3	b3 =8	a31= 1	a32= 1
R4	b4 =12	a41= 3	a42= 1

Решение. Построим математическую модель задачи.

Найти значения переменных x₁, x₂, удовлетворяющие условиям:

, (2.6)

при которых целевая функция принимает максимальное значение.

Решение проведем симплексным методом. Приведем систему к каноническому виду введением дополнительных переменных: ,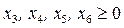

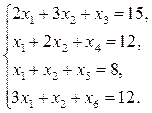(2.7)

Дополнительные переменные в данной задаче соответствуют остаткам ресурсов. В качестве основных (базисных) переменных выберем дополнительные переменные . Из каждого уравнения выразим основные переменные через неосновные:

(2.8)

Первоначальное базисное решение является допустимым. Значение целевой функции равно F₀=0.

Значение целевой функции 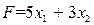может быть увеличено за счет увеличения значений переменных х₁ и х₂, так как эти переменные входят в линейную целевую функцию с положительными коэффициентами.

На втором этапе решения следует перейти к лучшему (не худшему) решению с помощью смены базиса. В новый базис следует перевести одну из переменных, которая входит в линейную целевую функцию с положительным коэффициентом. Переведем в основные переменные х₁, т.к. в целевой функции коэффициент при ней больше. Число базисных переменных всегда остается постоянным, поэтому одна из переменных старого базиса должна быть переведена в неосновные.

Увеличение значения переменной х₁ приведет к уменьшению переменных старого базиса, т.к. в выражения для этих переменных х₁ входит с отрицательными коэффициентами. Вычислим оценочные отношения для каждой переменной. Для этого разделим свободные члены в каждом выражении на модуль коэффициента при х₁. Если в каком-либо равенстве коэффициент при переменной, переводимой в базис, был бы положительным, то соответствующее оценочное отношение равнялось бы бесконечности (∞).

Оценочные отношения для полученной системы равны соответственно 15/2, 12, 8, 12/3. Чтобы решение оставалось допустимым (т.е. все переменные оставались неотрицательными) значение х₁ может быть увеличено до наименьшего значения: min{15/2, 12, 8, 12/3}=4. Уравнение, соответствующее этому оценочному отношению, из которого определяется ограничение на рост переменной х₁, называется разрешающим. Разрешающее уравнение подчеркнуто. Следовательно, переменную х₆ переводим в неосновные.

Выражая из разрешающего уравнения х₁ и подставляя в остальные уравнения, получим:

(2.9)

Целевая функция примет вид: 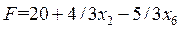. Новое базисное решение .

Значение целевой функции 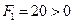. Произошло увеличение значения целевой функции, но в выражении для неё есть переменная х₂ с положительным коэффициентом. Т.е. увеличение переменной х₂ приведет к росту значения целевой функции.

Повторяем процедуру перехода к новому базису. Переведем х₂ в основные переменные. Значение х₂ может быть увеличено до min{12, 3, 24/5, 6}=3. При этом старые основные переменные останутся неотрицательными. Разрешающее уравнение подчеркнуто. Выразим из него х₂ и подставим в остальные уравнения:

(2.10)

Целевая функция примет вид: .

Новое базисное решение . Значение целевой функции .

Так как в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то в соответствии с критерием оптимальности найденное решение задачи отыскания максимума линейной функции является оптимальным.

Таким образом, продукция Р₁ должна быть выпущена в количестве 3 единиц, продукция Р₂ - в количестве 3 единиц. Остатки ресурсов R₁ и R₄ равны 0, а остатки ресурсов R₂ и R₃ равны 3 и 2 единицы соответственно.

Дата добавления: 2014-01-06