Решение двойственной задачи и определение интервалов устойчивости двойственных оценок оптимального решения

На основании полученного оптимального решения двойственной задачи можно провести анализ устойчивости решения относительно изменения запасов ресурсов. Т.е. можно определить, в каких интервалах допустимо изменять значения запасов ресурсов, чтобы двойственные оценки оставались неизменными.

Пример 11. При решении двойственной задачи, составленной в примере 9, симплексным методом, получаются следующие результаты.

Базисные переменные: y₁, y₄, неосновные переменные: y₂, y_3, y₅, y₆.

(2.48)

Предположим, что запасы b_i ресурсов каждого вида изменились на ∆b_i единиц (i=1, 2, 3, 4). Запишем исходное выражение целевой функции с новыми коэффициентами:

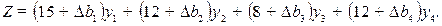(2.49)

Подставим в него полученные выражения для оптимальных решений у₁ и у₄, после преобразований получим:

(2.50)

Для того чтобы полученное решение двойственной задачи оставалось оптимальным, коэффициенты при неосновных переменных в целевой функции должны остаться неотрицательными:

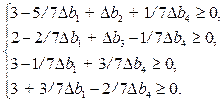(2.51)

В том случае, когда запасы изменяются одновременно по нескольким видам ресурсов, найти интервалы устойчивости как решение системы неравенств (2.51) в общем случае затруднительно. Однако можно проверить, удовлетворяют ли конкретные изменения запасов ресурсов системе (2.51).

Например, если 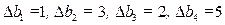, то решение останется оптимальным, т.к. все неравенства удовлетворены. При этом , вектор решения исходной задачи .

Если , то первое неравенство не выполнено. Переменная у₂ должна быть переведена в базисные переменные, и оптимальное решение изменится.

Определим интервалы устойчивости оптимального решения двойственной задачи по каждому ресурсу в отдельности.

1) Полагая 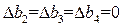, получаем систему неравенств

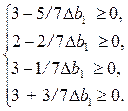(2.52)

Следовательно, решение останется оптимальным, если .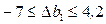

2) Полагая 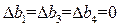, получаем неравенство

Следовательно, решение останется оптимальным, если .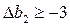

3) Полагая 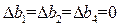, получаем неравенство .

Следовательно, решение останется оптимальным, если .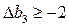

4) Полагая 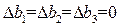, получаем систему неравенств

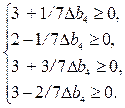(2.53)

Решение останется оптимальным, если .

Дата добавления: 2014-01-06