Задачи целочисленного программирования

Во многих практических задачах линейного программирования переменные по своему физического смыслу должны принимать только целочисленные значения. Такие задачи называют задачами целочисленного программирования.

Пусть требуется найти такое решение X=(x₁, x₂,…x_n), при котором линейная функция принимает максимальное или минимальное значение при ограничениях

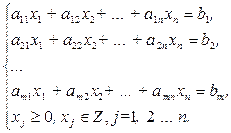(2.54)

Методы целочисленной оптимизации можно разделить на 3 группы: методы отсечения, комбинаторные методы, приближенные методы. Из методов отсечения наиболее часто используется метода Гомори, из комбинаторных методов – метод ветвей и границ. Рассмотрим подробнее алгоритм метода отсечения Гомори.

1. Задача линейного программирования решается симплексным методом без учета условия целочисленности.

2. Если все компоненты оптимального решения целые, то решение является оптимальным и для задачи целочисленного программирования.

3. Если среди компонент оптимального решения есть нецелые, то к ограничениям задачи добавляют новое ограничение, удовлетворяющее следующим условиям: оно должно быть линейным, должно отсекать найденный оптимальный нецелочисленный план, не должно отсекать ни одного целочисленного решения. Такое ограничение называется правильным отсечением.

Пусть задача линейного программирования имеет конечный оптимум и на последнем шаге ее решения симплексным методом получены уравнения, выражающие основные переменные x₁, x₂,…x_m через неосновные x_m+1, x_m+2,…x_n оптимального решения:

(2.55)

Пусть в оптимальном решении 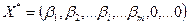– нецелая компонента. Тогда неравенство

(2.56)

где {} – дробная часть числа, обладает свойствами правильного отсечения.

4. Введением дополнительной неотрицательной переменной неравенство (2.56) преобразуется в уравнение

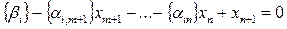(2.57)

и включается в систему ограничений (2.54). Это равносильно добавлению уравнения (2.57) к системе (2.55).

5. Полученная расширенная задача решается симплексным методом. Если её оптимальное решение будет целочисленным, исходная задача решена. В противном случае алгоритм повторяется с п.3.

Если задача разрешима в целых числах, то оптимальный целочисленный план будет найден за конечное число шагов.

Если в процессе решения появится уравнение, выражающее основную переменную через неосновные, с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. Следовательно, и вся задача не имеет целочисленного оптимального решения.

Пример 12. Пусть имеется определенная сумма денег (20000 р.) и её можно потратить на покупку топлива. Поставщик продает топливо в емкостях двух различных объёмов: больших бочках по 200 литров и канистрах по 20 литров. Стоимость пустой тары: бочка – 600 р., канистра – 100 р. Стоимость литра топлива – 25 р. Необходимо определить оптимальное количество бочек и канистр, чтобы количество литров топлива в них было максимальным.

Решение. Составим математическую модель задачи.

Пусть x₁ – количество бочек, x₂ – количество канистр. Целевая функция: . Запишем ограничения:

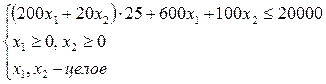(2.58)

Решая задачу симплексным методом без учета целочисленности переменных x₁ и x₂, получаем:

(2.59)

Решение является оптимальным, но нецелочисленным: .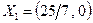

Строим правильное отсечение:

. (2.60)

После добавления неравенства (2.60) к решению (2.59) и введения дополнительной переменной x₄, имеем:

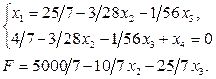(2.61)

Продолжая решение симплексным методом, получаем:

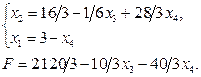(2.62)

Решение является оптимальным, но нецелочисленным: .

Строим правильное отсечение по уравнению, соответствующему нецелочисленной компоненте решения:

. (2.63)

После добавления неравенства (2.63) к решению (2.62) и введения дополнительной переменной x₅, имеем:

(2.64)

Продолжая решение симплексным методом, получаем:

(2.65)

Получено оптимальное целочисленное решение: , F_max =700.

Ответ: для покупки максимального количества топлива нужно купить 3 бочки и 5 канистр.

Замечание: неосновная переменная x₄ не входит в выражение целевой функции на оптимальном решении, следовательно, ее изменение не изменяет значения F_max. Но для того, чтобы решение оставалось допустимым, переменная x₄ может принимать значения от 0 до ½. Только при x₄ =0 решение задачи является целочисленным.

Тема 3. Транспортная задача

Дата добавления: 2014-01-06