Экономико-математическая модель транспортной задачи

Среди задач линейного программирования особое место занимает так называемая транспортная задача. В общем виде она формулируется следующим образом.

Имеется m поставщиков некоторой продукции и n потребителей этой продукции. Известны мощности поставщиков (запасы продукции) и спросы потребителей, а также удельные затраты на перевозку единицы продукции по каждому маршруту «поставщик – потребитель». Необходимо найти объемы перевозок для каждого маршрута так, чтобы суммарные затраты на перевозку были минимальными.

Например, пусть некоторая фирма занимается переработкой сельскохозяйственной продукции на нескольких (n) заводах, расположенных в разных населенных пунктах. Продукция поставляется сельхозпредприятиями с нескольких (m) складов, расположенных в районах области.

Предположим, что стоимость продукции одинаковая, но перевозка со склада i на завод j зависит от расстояния и отличается для маршрута. Если стоимость продукции различна, будем считать, что это различие учитывается в транспортных затратах. Месячная потребность заводов в продукции различна, и запасы на каждом складе в течение месяца ограничены.

Требуется определить, какое количество продукции необходимо перевозить по каждому маршруту склад i – завод j в данном месяце для минимизации общих затрат на перевозку.

Введем следующие обозначения: x_ij – количество продукции, перевозимой со склада i на завод j (по маршруту i-j), c_ij – удельные затраты на перевозку единицы продукции по этому маршруту, A_i – запасы на i -м складе (мощность, или запасы, поставщика), B_j – потребность j -го завода (мощность, или спрос, потребителя), F – суммарные затраты на перевозку продукции по всем маршрутам (целевая функция), Y_i – количество продукции, фактически перевезенной с i -го склада, Z_j – количество продукции, фактически перевезенной на j -й завод.

Необходимо найти оптимальные значения x_ij, удовлетворяющие системе ограничений:

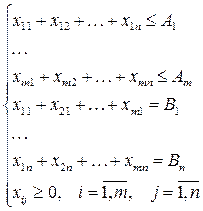(3.1)

при которых целевая функция принимает наименьшее значение:

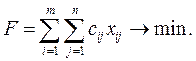(3.2)

Сформулированная задача является вариантом задачи линейного программирования. При этом она имеет некоторые особенности:

1. Коэффициенты при переменных в системе ограничений (3.1) равны 1 или 0.

2. Каждая переменная входит ровно в два ограничения.

Можно было бы применить изученный симплексный метод для решения такой задачи, однако в теории исследования операций разработан специальный метод решения транспортных задач. Подробно метод решения изложен в учебнике [1]. Кратко отметим основные этапы решения.

При решении придерживаются следующего алгоритма.

Шаг 1. Проверить баланс мощностей поставщиков и потребителей. При этом возможны три случая:

А) Если , то задача является закрытой (суммарные мощности поставщиков и потребителей равны, вся продукция будет перевезена со складов на заводы, все запросы заводов будут удовлетворены).

Б) Если 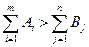, то задача является открытой. Суммарная мощность поставщиков больше суммарной мощности потребителей. Для приведения задачи к закрытой необходимо ввести фиктивного потребителя (n +1) с мощностью 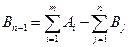, соответствующие удельные затраты c_{i,(n+ 1 )} равны нулю.

В) Если 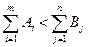, то задача также является открытой. Суммарная мощность поставщиков меньше суммарной мощности потребителей. Для приведения задачи к закрытой необходимо ввести фиктивного поставщика (m +1) с мощностью 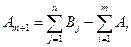, соответствующие удельные затраты c_{(m+ 1 ), j} равны нулю.

Для закрытой задачи система ограничений (3.1) состоит только из равенств. Поэтому далее решается задача определения переменных x_ij, удовлетворяющие системе ограничений 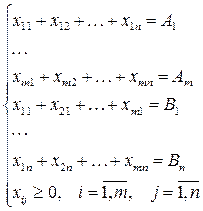(3.3).

(3.3)

при которых целевая функция принимает наименьшее значение:

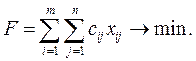(3.4)

Система (3.3) состоит из (m+n) уравнений, но т.к. в случае закрытой задачи сумма первых m уравнений равна сумме последних n уравнений, то только (m+n – 1) из уравнений системы являются линейно-независимыми. Число базисных переменных задачи линейного программирования (3.3) – (3.4) равно (m+n – 1).

Шаг 2. Выполнить первоначальное распределение поставок, т.е. определить начальные значения переменных x_ij. Тем самым определяется базисное решение, которое всегда является допустимым.

Шаг 3. Проверить полученный план поставок на оптимальность, в случае необходимости организовать пересчет плана.

Проверка плана на оптимальность проводится методом потенциалов по значениям так называемых оценок клеток. Отметим, что оценки клеток по сути являются коэффициентам при неосновных переменных целевой функции. Т.к. транспортная задача – это задача минимизации целевой функции, то критерием оптимальности полученного плана поставок является неотрицательность оценок свободных клеток. Пересчет плана выполняется в том случае, когда имеются клетки с отрицательными оценками. Он соответствует переходу к новому базисному решению.

Если среди свободных клеток есть клетки с нулевыми оценками, то задача имеет неединственное оптимальное решение.

Рассмотрим подробно решение транспортной задачи на примере.

Дата добавления: 2014-01-06