Наращение по сложным процентным ставкам

Сложные проценты

В финансовой практике значительная часть расчетов ведется с использованием схемы сложных процентов.

Применение схемы сложных процентов целесообразно в тех случаях, когда:

– проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;

– срок ссуды более года.

Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга:

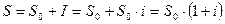– за один период начисления;

– за два периода начисления;

отсюда, за 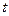периодов начисления формула примет вид:

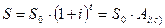- формула процентов, т.е. 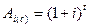- множитель наращения;

где 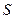– наращенная сумма долга;

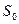– первоначальная сумма долга;

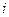– ставка процентов в периоде начисления;

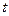– количество периодов начисления;

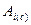– коэффициент (множитель) наращения сложных процентов.

Рост по сложным процентам представляет собой процесс, соответствующий геометрической прогрессии, первый член которой равен 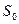, а знаменатель – 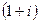. Последний член геометрической прогрессии равен наращенной сумме в конце срока ссуды.

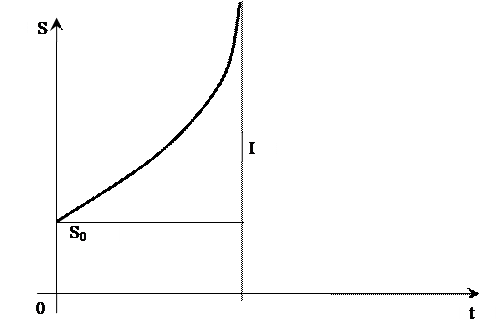
Рисунок 5 – Наращение по сложным процентам

Коэффициенты (множители) наращения, зависящие от процентной ставки и числа периодов наращения, табулированы (см. приложение B). Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через 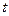периодов при заданной процентной ставке .

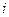При выводе формулы 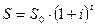предполагалось, что 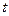измеряется в годах, а 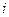является годовой процентной ставкой. Однако эту формулу можно применять и для других периодов начисления – для месяцев, полугодий, дней и т. д. При этом нужно обязательно следить, чтобы длина периода и процентная ставка имели временное соответствие.

– Если срок контракта равен 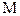месяцев, а 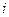- годовая процентная ставка, то в формуле наращенной суммы величину 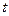нужно выразить как 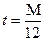- часть года, тогда наращенная сумма по сложной процентной ставке составит: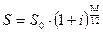

– Если срок контракта равен 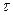дней, то в формуле наращенной суммы 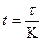- часть года, тогда наращенная сумма по сложной процентной ставке составит: .

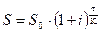Время при наращении по сложной ставке обычно измеряется как .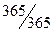

Пример 14: Депозит в 200 тыс. руб. положен в банк на 4 года под 15% годовых. Найти наращенную сумму, если ежегодно начисляются сложные проценты.

Решение: Применяя формулу 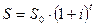, получим:

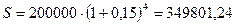руб.

Пример 15: На банковский счет положены 200000 на 3 месяца по ставке 36% в год. Найти наращенную сумму по сложным процентам.

Решение: Воспользуемся формулой 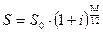. Помучаем: 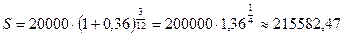руб.

Пример 16: Сумма 10000 рублей положена на банковский счет сроком на 73 дня по ставке 10% в год. Найти наращенную сумму по сложным процентам.

Решение: Применяя формулу 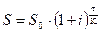получим: 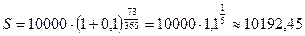руб.

Пример 17. Сумма в размере 2000 долларов дана в долг на 2 года по ставке процента равной 10% годовых. Определить проценты и сумму, подлежащую возврату.

Решение: Наращенная сумма 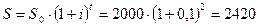долларов

или 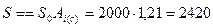долларов,

где 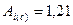(приложение B).

Сумма начисленных процентов 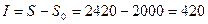долларов. Таким образом, через два года необходимо вернуть общую сумму в размере 2420 долларов, из которой 2000 долларов составляет долг, а 420 долларов – "цена долга".

Дата добавления: 2014-01-06