
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №7 Типовые звенья САУ
|
|
|
|
Вопросы
- В чем заключается принцип суперпозиции?
- Для чего используются передаточные функции системы?
- Перечислите частотные функции?
- В чем физический смысл функции Грина?
- В чем отличие Логарифмических частотных характеристик, от частотных.
Элементарные звенья и их характеристики (типовые звенья)
Из курса алгебры известно, что полином произвольного порядка можно разделить на простые множители вида: S, (S+d1), (S2+d1S+d2). Поэтому любую дробно рациональную передаточную функцию можно представить в виде элементарных множителей и элементарных дробей вида 1/S, 1/(S+d1), 1/ (S2+d1S+d2). Звенья, передаточные функции которых представляются элементарными множителями или элементарными дробями, называются элементарными.
Элементарные множители первого и второго порядка приводятся к стандартному виду, принятому в теории автоматического управления.
K/(TS+1), K/(T2S2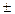 2xTS
2xTS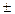 1), 0
1), 0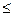 x
x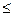 1.
1.
При этом К (К>0) называют передаточным коэффициентом, T(T>0) - постоянной времени (имеет единицу измерения времени), x- коэффициентом демпфирования.
Полиномы числителя и знаменателя передаточной функции можно разложить на простейшие множители по их корням.

здесь μ = b0/a0 – константа.
Возможны два случая:
• Корни вещественные. Оставляем скобки без изменения.
• Пара комплексно - сопряженных корней вида: p1,2= α ± j β - объединяем их и раскрываем скобки (p- α +j β )(p- α -j β )= p2-2 α p + β 2 + α 2 -полином имеет вещественные коэффициенты.
После такого представления в числителе и знаменателе будет некоторое количество скобок первого порядка, соответствующих вещественным корням, и некоторое количество скобок второго порядка, соответствующих комплексно – сопряженным корням. При этом все числовые коэффициенты в скобках будут вещественными.
Рассмотрим каждую такую скобку, как элементарную передаточную функцию, практически реализуемую в силу вещественности коэффициентов.
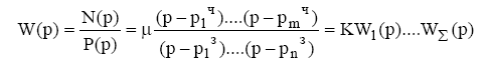 (7.1)
(7.1)
Σ = n+m, если все корни вещественные;
Σ < n+m, если есть комплексные корни.
Принято выносить общий множитель К за скобки так, чтобы свободный член всех скобок был равен 1. Тогда К называют коэффициентом усиления. Заметим, что W(0) = К = bm/an. Это значит, что К есть коэффициент усиления на нулевой частоте -"постоянном токе".
Итак, любая Wi (р) может быть одного из следующих видов:
1. К - Усилительное звено;
2. p - Дифференцирующее звено;
3. 1/p - Интегрирующее звено (интегратор);
4. K/(Tp+1) - Инерционное (апериодическое) звено;
5. K/(T2p+2dTp+1) - Колебательное звено;
6. K(Tp+1) - Форсирующее звено;
7. K(T2p+2dTp+1) - Форсирующее звено 2-го порядка.
Замечание:
форсирующее звено (4) является комбинацией (суммой) усилителя и дифференциатора;
звенья (2), (6), (7) не являются, в строгом смысле, реализуемыми.
Статические и астатические системы
Большинство функциональных элементов систем автоматического управления обладают свойствами апериодичных, а также без инерционных звеньев. Помимо этих звеньев обычно в состав систем входят несколько интегрирующих и форсирующих звеньев.
Таким образом, типовая передаточная функция разомкнутого контура САУ может быть представлена в виде:
W(р.)= m < n, (7.2)
m < n, (7.2)
где n - порядок дифференциального уравнения системы;
r - количество интегрирующих звеньев;
m - количество форсирующих звеньев;
K - коэффициент передачи системы по 2-ой производной входного воздействия.
Для типовых систем автоматического управления:
m=1; r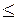 2.
2.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 920; Нарушение авторских прав?; Мы поможем в написании вашей работы!