
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критерий Михайлова
|
|
|
|
Для того чтобы система была устойчива необходимо и достаточно, чтобы кривая Михайлова, начинаясь при a0>0 с действительно положительной полуоси, при возрастании  последовательно обходила n квадрантов, в положительном направлении, не попадая в начало координат (рис. 8-1).
последовательно обходила n квадрантов, в положительном направлении, не попадая в начало координат (рис. 8-1).
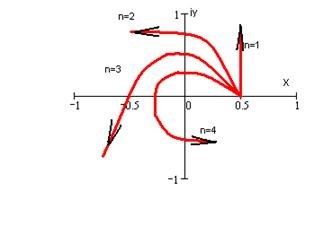
Рисунок 10‑1 Годограф Михайлова
Пример: Характеристический полином.
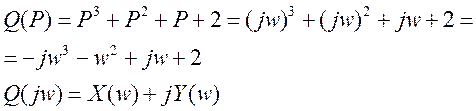
Составим таблицу
| w | 0< w <1 | 1< w <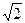
| w> 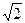
| 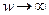
| ||
| X(w) | >0 | >0 | <0 | 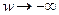
| ||
| Y(w) | >0 | <0 | <0 | 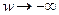
|
Построим кривую Михайлова. В пределах квадранта всей кривой Михайлова на устойчивость не влияет, и она строится приблизительно. Система неустойчива, т.к. кривая не охватывает последовательно 1, 2, и 3 квадрант.
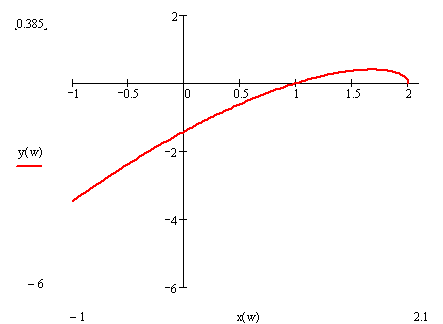
Рисунок 10‑2 – Годограф Михайлова
Пример. Характеристический многочлен 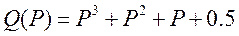
Для 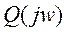 имеем
имеем 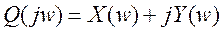
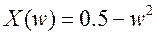 ,
, 
Составим таблицу
| w | 0< w <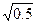
| 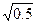
| 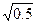 < w <1 < w <1
| 1 | w> 1 | 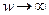
| |
| X(w) | 0,5 | >0 | <0 | -0,5 | <0 | 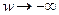
| |
| Y(w) | >0 | 0,35 | >0 | <0 | 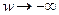
|
Построим кривую Михайлова

Рисунок 10‑3 Годограф Михайлова
Кривая последовательно охватывает все 3 квадранта, следовательно, система будет устойчивой.
Алгебраические критерии устойчивости и критерий Михайлова применимы для исследования замкнутой и разомкнутой систем.
Есть критерий, который предназначен для исследования лишь замкнутых систем. Этот критерий был сформулирован Найквистом.
Критерий Найквиста
Пусть l из корней разомкнутой системы находится в правой полуплоскости, а остальные n-l в левой полуплоскости. Тогда, для того, чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика её разомкнутой системы с ростом w от 0 до 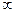 охватывала точку (-1,j0) в положительном направлении, т.е. против движения часовой стрелки в (l /2) раз.
охватывала точку (-1,j0) в положительном направлении, т.е. против движения часовой стрелки в (l /2) раз.
В частности, если разомкнутая система устойчива (и, следовательно, l=0), то для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика её разомкнутой системы охватывала точку (-1, j0) в положительном направлении l/2 раза.
Пример: частотная передаточная функция её разомкнутой системы 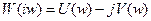
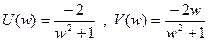
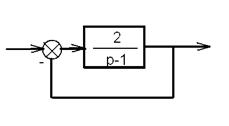
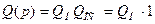
Составим таблицу.
| w | w>0 | 
| |
| U(w) | -2 | <0 | 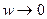
|
| V(w) | <10 | 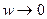
|

Рисунок 10‑4 Годограф Найквиста
Амплитудно – фазовая частотная характеристика разомкнутой системы охватывает точку (-1, j0) в положительном направлении ½ раза. Характеристическое уравнение разомкнутой системы имеет 1 корень, т.е. l=1, поэтому замкнутая система устойчива.
Примеры:
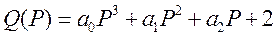
Варианты:
| a0 | a1 | a2 | a3 |
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 819; Нарушение авторских прав?; Мы поможем в написании вашей работы!