Решение систем линейных уравнений

Поиск минимального и максимального элементов массива

Вычисление сумм элементов массивов

Задача 9.4.5. Вычислить сумму элементов одномерного массива.

Решение.

S=0

FOR j = 1 TO n

S=S+ A(i)

NEXT j

PRINT S

Задача 9.4.6. Вычислить сумму нечетных элементов двухмерного массива.

Решение. Элемент массива считается четным, если сумма его индексов четная, и наоборот – элемент массива считается нечетным, если сумма индексов элемента массива нечетная. Например, A(0,0), A(1,5) – четные элементы массива, а элементы А(0,1), А(4,7) – нечетные. Поэтому для определения суммы нечетных элементов массива необходимо в цикле подсчитывать сумму индексов элемента массива и проверять, является эта сумма четной или нечетной. Для проверки четности суммы индексов можно использовать арифметический оператор MOD (см. раздел 7.1.4.).

S=0

FOR i = 1 TO n

FOR j = 1 TO m

k=i+j

IF k MOD 2 <>0 THEN S=S+ A(i, j)

NEXT j

NEXT i

PRINT S

Задача 9.4.7. Найти максимальный и минимальный элементы одномерного массива.

Решение. При поиске минимального и максимального значений элементов массива в качестве начального значения вспомогательным переменным Amax и Amin необходимо присвоить значение любого элемента массива, например, нулевого:

Amax=A(0): Amin=A(0)

FOR i = 1 TO n

IF A(i)>Amax THEN Amax=A(i)

IF A(i)<Amin THEN Amin=A(i)

NEXT i

PRINT “Amax =“;Amax, “Amin=”;Amin

Сортировка массивов

Одной из операций с массивами является сортировка данных.

Известно много различных способов сортировки массивов. Однако, независимо от используемого способа в программе осуществляется сравнение текущего элемента массива с другим элементом этого же массива и, в зависимости от результатов сравнения, осуществляется обмен данными между этими элементами. Qbasic имеет полезную функции SWAP, которая предназначена для обмена значениями двух переменных.

Самая простая процедура сортировки – перебор.

FOR = i=1 To n - 1

FOR j = i + 1 To n

IF A(j) < A(i) THEN SWAP A(i), A(j)

NEXT j

NEXT i

Приведенная процедура обеспечивает сортировку по возрастанию значения элементов массива. Для сортировки элементов массива по убыванию их значений достаточно поменять знак отношения в третьей строке.

Системой линейных уравнений с n неизвестными x₁, х₂,..., х_n называется система вида:

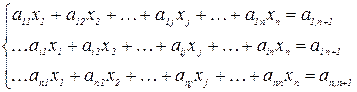(9.4.27)

Здесь a_ij — коэффициенты при неизвестных, a_i,n+1 — свободные члены.

Индекс i означает номер уравнения, j — номер неизвестного.

Решением системы (9.4.27) называется совокуп­ность таких значений переменных с₁,..., с_n , при под­становке которых в данную систему каждое уравнение системы обращается в числовое равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Две системы уравне­ний называются эквивалентными, если множество их решений совпадают. Преобразования, переводящие одну систему в эквивалентную ей систему, называются эквивалентными.

Перестановка двух уравнений системы, умножение уравнения системы на любое число, отличное от нуля, прибавление к уравнению другого уравнения, умножен­ного на любое число, отличное от нуля, являются экви­валентными преобразованиями.

Одним из распространенных методов решения сис­тем линейных уравнений является метод Гаусса (метод исключений). Методом Гаусса получают аналитические выражения для вычисления точных значений переменных. В ос­нове метода лежит прием последовательного исключе­ния переменных для получения эквивалентной треу­гольной или трапецеидальной системы уравнений. Для решения системы уравнений методом Гаусса с использованием ЭВМ необходимо на основании исход­ной системы уравнений (9.4.27) составить матрицу ко­эффициентов и свободных членов - расширенную матрицу.

Рассмотрим пример решения системы методом Гаусса на основе системы третьего порядка. Составим расширенную матрицу:

a₁₁ a₁₂ a₁₃ b₁

a₂₁ a₂₂ a₂₃ b₂ (9.4.28)

a₃₁ a₃₂ a₃₃ b₃

Прямой ход.

Сначала с помощью первого уравнения исключается х₁ из второго и третьего уравнений. Для этого каждый элемент первой строки разделим на коэффициент а₁₁, умножим на коэффициент а₂₁ и вычтем полученные значения из соответствующих элементов второй строки:

a’₂₂=а₂₂ – a₁₂/a₁₁*a₂₁, a’₂₃=а₂₃ – a₁₃/a₁₁*a₂₁, b’₂=b₂– b₁/a₁₁*a₁₂

а’₃₂ =а₃₂ – a₁₂/a₁₁*a₃₂, а’₃₃ =а₃₃ – a₁₃/a₁₁*a₃₃, b’₃=b₃– b₁/a₁₁*a₁₃

или в общем виде:

a_ij=a_ij – a_i1/a₁₁*a_1j i = 2, 3, j = 2, 3

b_i = b_i – b₁/a₁₁*a_1i, i = 2,3.

Аналогично с помощью второго уравнения исключается х₂ из третьего уравнения:

а’’₃₂ =а’₃₂ – a’₂₂/a’₂₂*a’₃₂, а’’₃₃ =а’₃₃ – a’₂₃/a’₂₂*a’₃₃, b’’₃=b’₃– b’₂/a’₂₂*a’₂₃

В результате получим треугольную матрицу:

a₁₁ a₁₂ a₁₃ b₁

0 a’₂₂ a’₂₃ b’₂

0 a’’₂₃ a’’₃₃ b’’₃

Обратный ход.

Обратный ход начинается с решения третьего уравнения системы:

x₃ = b’’₃/a’’₃₃.

Используя это значение можно найти х₂ из второго уравнения, а затем х₁ из первого уравнения:

x₂=(b’₂ - a’₂₃*x₃)/a’₂₂; x₁=(b₁ - a₁₂*x₂ - a₁₃*x₃)/a₁₁.

В данном примере предполагалось, что все коэффициенты матрицы не нулевые. На практике необходимо проверять, чтобы элемент матрицы, на который производится деление не был нулевым. Если ведущий элемент матрицы равен нулю, то необходимо сделать перестановку строк матрицы.

Известны численные методы решения систем линей­ных уравнений, например метод простых итераций. Численные методы дают приближенное решение систе­мы уравнений. Однако при большом числе переменных, например п > 100, сложность метода итераций меньше сложности метода Гаусса.

Дата добавления: 2014-01-06