Интерполирование функций

Программа решения системы уравнений методом Гаусса

Входные данные:

N — количество уравнении и неизвестных (степень системы уравнений);

A (N,N+1) — матрица коэффициентов и свобод­ных членов (расширенная матрица системы уравне­ний).

Вспомогательный массивы C(N).

Выходные данные: X(N) — решение системы

INPUT “Укажите степень системы уравнений ”,N

DIM A(N,N+1), C(N), X(N)

REM Ввод коэффициентов расширенной матрицы

FOR i=0 TO N

FOR j=0 TO N+1

PRINT “Введите коэффициент а(“I”,”j”) ”;

INPUT “ ”,A(i,j)

NEXT j

NEXT i

REM Начало цикла вычислений

FOR K=0 TO N-1

REM Процедура перестановки строк

IF A(K,K)<>0 THEN GOTO 7070

FOR P=K+1 TO N

IF A(P,K)>=1E-08 THEN GOTO 7030

NEXT P

PRINT "НЕТ РЕШЕНИЯ"

7015 STOP

7020 GOTO 7100

7030 FOR J=K TO N+1

R=A(K,J)

A(K,J)=A(P,J)

A(P,J)=R

NEXT J

‘ Конец процедуры перестановки строк

REM Прямой ход

7070 FOR I=K+1 TO N

B=A(I,K)/A(K,K)

FOR J=K TO N+1 ‘ вычисление коэффициентов

A(I,J)=A(I,J)-B*A(K,J)

NEXT J

NEXT I

NEXT K

REM Обратный ход

X(N)=A(N,N+1)/A(N,N)

FOR K=N-1 TO 0 STEP -1

R=0

FOR J=K+1 TO N

R=R+A(K,J)*X(J)

NEXT J

X(K)=(A(K,N+1)-R)/A(K,K)

NEXT K

GOTO 7020

PRINT "ОШИБКА": GOTO 7015

7100 REM вывод результата

FOR i=0 TO N

PRINT X(i)

NEXT i

END ‘ конец программы

При решении многих задач значения функции задаются в виде двухмерной таблицы, в одной строке которой задаются значения аргумента, а в другой соответствующие значения функции. Точки, в которых определены значения функции называются узлами интерполяции. Но этого бывает недостаточно и требуется найти значения функций в некоторых точках, отличных от узлов интерполяции. Вычисление значения функции f(x) в точках х, отличных от узлов интерполяции, называется интерполяцией.

Методы интерполяции используются в управляю­щих ЭВМ для сокращения времени вычислений. Нап­ример, требуемое состояние технологического процесса можно задать в виде таблицы значений функций в кон­трольных точках. Значение текущих параметров про­цесса рассчитывается ЭВМ с использованием указан­ных методов.

Для поиска значений функции в точках, отличных от узлов интерполяции, необходимо построить функцию F, принимающую в узлах интерполяции те же значения, что и функция f(х), то есть F(x₀) = f(x₀), F(x₁) = f(x₁),..., F(x_n) = f(x_n). Таких функций может быть построено бесконечное множество.

Способ построения функции F, принимающей в узлах интерполяции те же значения, что и функция f, называется интерполированием, а функцию F называ­ют интерполирующей функцией. Геометрически интер­полированию соответствует нахождение плавной кри­вой, проходящей через заданные точки (х_i ; f(x_i)) (рис. 9.4.11). Так как таких кривых может быть бесчисленное множество, то задача отыскания интерполирующей функции в общей постановке не решается однозначно. В качестве интерполирующей функции обычно исполь­зуется полином Лагранжа, многочлен Ньютона, непре­рывные дроби, многочлен вида Рп(х) == a₀ xⁿ + a₁ х^n-1 +... + a_n-1 x + а_n. Наибольшей простотой с точки зрения вы­числения обладают интерполяционный полином Лаг­ранжа и интерполяци­онный многочлен Ньютона.

Интерполяционный многочлен Лагранжа имеет следующий вид:

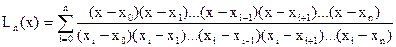. (9.4.29)

При n=1 получаем формулу для линейной интерполяции:

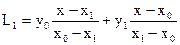. (9.4.30)

Для ускорения вычислений многочлена при различных значениях n применяют схему Эйткена, в которой не требуется явного построения многочлена:

,

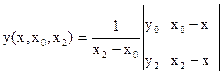, (9.4.31)

.

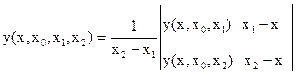Теперь для вычисления значения функции в произвольной точке числовой оси не совпадающей с узлами интерполяции следует вычислить y(x)=L_n(x).

Дата добавления: 2014-01-06