Основные свойства эвольвенты

Эвольвентой окружности называется плоская кривая, которую описывает любая точка прямой линии, катящейся по окружности без скольжения. Эвольвента – это спиралеобразная кривая, имеющая две ветви с точкой заострения на основной окружности.

Прямая, обкатывающаяся без скольжения по основной окружности, называется производящей прямой.

Окружность, по которой катится прямая линия, образующая эвольвенту, называется основной окружностью (основа эвольвенты).

Стандартное обозначение радиуса основной окружности - r_b.

Боковая поверхность зуба представляет собой звольвентную поверхность, которую образует траекто­рия прямой линии находящейся на плоскости, катящейся по основному цилиндру без скольжения. Образование эвольвентной поверхности может быть представлено следующим образом. На барабан (основной цилиндр) на­мотана лента. Если с неподвижного барабана сматывать ленту, то конец ленты (и любая прямая на ленте) будет описывать эвольвентную поверхность.

1. Эвольвента не имеет точек внутри основной окружности. Прямая, образующая эвольвенту, катится по внешней стороне основной окружности и внутри ее не может быть точек эвольвенты. Точка А₀ - начало эволь­венты на основной окружности.

2. Форма эвольвенты полностью определяется радиусом основной окружности r_b и не зависит от ос­тальных параметров. Если мы возьмем другую прямую или другую точку на прямой, то она опишет точно та­кую же траекторию - эвольвенту. Все эвольвенты одной и той же основной окружности одинаковы.

3. Нормаль к эвольвенте в любой ее точке касательна к основной окружности. Докажем это.

Проведем основную окружность радиуса r_b с центром в точке О (рис. 5). С точки А₀ построим эволь­венту. Через произвольную точку М на эвольвенте проведем касательную к основной окружности. Точку каса­ния обозначим N. Так как образующая прямая катится по неподвижной окружности, то точка N является мгновенным центром скорости точки М, а, следовательно, MN - мгновенный радиус вращения точки М. Скорость пер­пендикулярна MN- мгновенному радиусу вращения. Но в то же время является касательной к траектории

точки М - эвольвенте. MN ^, а это значит, что касательная к основной окружности является нормалью к эвольвенте.

Рисунок 5 - Свойство нормали к эвольвенте

4. Радиус кривизны эвольвенты в любой ее точке равен отрезку нормали, заключенном между эвольвентой и точкой касания нормали с основной окружностью. Это свойство вытекает из предыду­щего. Абсолютная линейная скорость точки М перпендикулярна радиусу кривизны МN траектории точки М. Следовательно MN = r_м. В любой другой точке М_i радиус кривизны r_i равен отрезку М_iN_i. В точке А₀ радиус кривизны эвольвенты равен нулю. Это точка заострения эвольвенты.

5. Расстояния по нормали между двумя эволвентами одной и той же основной окружности всюду одинаковы и равны расстоянию между началами эвольвент по дуге основной окружности. Изо­бразим две одноименные эвольвенты Э₁ и Э₂ одной и той же основной окружности, образованные двумя точками А и В одной и той же образующей прямой (рис. 6). Если образующую обкатывать в обратном направлении

по основной окружности, то в некоторый момент времени точки А₂,В₂ совместят­ся с точками а₁, B₁, а затем с точками А₀,В₀. Следовательно:

.

В₀

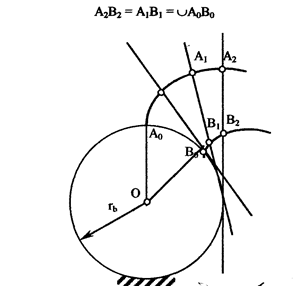
Рисунок 6 - Расстояния между эвольвенты по нормалям

6. Расстояния между двумя одноименными эвольвентами, измеренные по дугам концентриче­ских окружностей, пропорциональны радиусам этих окружностей.

Изобразим основную окружность радиуса r_b с центром О. Построим две одноименные эволь­венты Э₁ и Э₂ с началом их в точках А₀, В₀ (рис. 7). Проведем концентрическую окружность радиуса r₁ и точки пересечения ее с эвольвентами обозначим A₁, B₁. Соединим все точки с центром окружности О. Повернем эвольвенту Э₂ до совмещения с эвольвентой Э₁. Поскольку это одноименные эвольвенты, то при совмещении точек А₀ с В₀ должны совместится точки A₁ и В₁. Следовательно угол поворота точки В₀ по дуге основной окружности до совмещения с точкой А₀ (j) должен быть равен углу поворо­та точки В₁ по дуге окружности радиуса r₁ до совмещения с точкой а₁.

Рисунок 7 — Расстояния между эвольвентами по дугам концентрических окружностей

Определим длины дуг через их радиусы и углы поворота (в радианах):

.

,

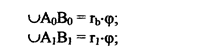
Эта зависимость применяется для определения шага зубьев эвольвентного колеса по дугам различных окружностей.

7. Угол давления эвольвенты в любой ее точке – это угол между направлением силы нормаль­ного давления и направлением абсолютной скорости данной точки.

Изобразим основную окружность радиуса r_b с центром в точке О и построим эвольвенту с на­чалом в точке а₀ (рис. 8). Точку А₀ соединим с центром О основной окружности. На эвольвенте выбе­рем некоторую произвольную точку A₁. Передача движения при зацеплении эвольвент происходит за счет сил давления. Сила давления направлена по нормали к контактирующим профилям (касательной к основной окружности). Проведем нормаль n-n и изобразим вектор силы давления Р. Точку касания нормали к основной окружности В₀ соединим с О. Абсолютная скорость точки A₁, если колесо враща­ется вокруг центра О с угловой скоростью w, направлена по касательной к траектории точки - окруж­ности радиуса r_x(OА₁). Соединим A₁ с центром О и в точке A₁ приложим вектор скорости 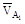. Угол

между направлением силы Р и скорости 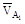обозначим a_х (угол давления).

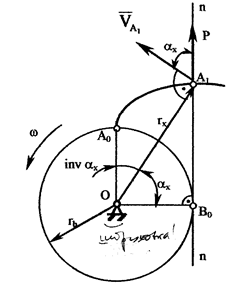
Рисунок 8 – Угол давления эвольвенты

Рассмотрим центральный угол Ð A₁OB₀. Этот угол равен углу давления a_x, так как стороны его пер­пендикулярны направлениям векторов силы и скорости: OA₁^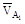; OB₀ ^ . Таким образом, центральный угол

между радиусом, проведенным в точку касания нормали к эвольвенте с основной окружностью, и радиусом, проведенным в данную точку эвольвенты, равен углу давления.

В точке А₀ угол давления равен нулю.

Дата добавления: 2014-01-06