Приближенный метод образования боковой поверхности

Этот метод основан на способе Тредгольда (1788-1829) – английского инженера – который состоит в следующем: вместо сферической эвольвенты строится кривая, расположенная на конической поверхности, которая касается поверхности сферы. Установлено, что при небольшой высоте зуба эти кривые мало отличаются одна от другой. Преимущество рассмотрения кривых, расположенных на конусах, состоит в том, что конус можно развернуть на плоскость.

Возьмем делительные (они же начальные) конусы (рис.3). Р – точка пересечения образующей делительного конуса с наружной (внешней) торцевой поверхностью зуба.

Размеры зуба конического колеса уменьшаются от наружного торца к внутреннему. Стандартный модуль (из ряда для прямозубых передач) назначают для внешнего торцевого сечения зубьев. Поэтому диаметры делительных окружностей для внешнего сечения

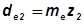; . (4)

Наружная поверхность зуба выполняется не по сфере радиуса ОР, а по дополнительному конусу, который имеет общую ось с соответствующим начальным конусом и касается сферы по окружности радиуса О₁Р (для первого колеса) и О₂Р (для второго колеса).

Дополнительные конусы имеют общую образующую О₁’Р и О₂’Р и общую касательную плоскость, проходящую через эту образующую.

Развертываем поверхности дополнительных конусов на плоскость, касательную к ним. Развертки представляют собой зубчатые секторы, касающиеся один другого в точке Р. Радиусы начальных окружностей равны

; . (6)

Рисунок 3 – Схема конического колеса

На данных развертках строится эвольвентное плоское зацепление с углом зацепления a_w=a=20° и по нему судят о качественных характеристиках конической передачи: о коэффициенте перекрытия, об отсутствии подрезания, об отсутствии интерференции и т.д.

Связь между действительными числами зубьев конических колес находится из условия, что шаг

является одинаковым для условных (приведенных) колес и действительных.

	.

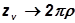
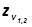– эти числа зубьев называют приведенными.

; . (7)

Очевидно, что передаточное отношение приведенных (эквивалентных) прямозубых колес не равно реальному передаточному отношению

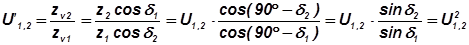. (8)

Таким образом зацепление конических колес эквивалентно зацеплению цилиндрических колес, но с большим числом зубьев. Поэтому при равных условиях конические колеса обладают большим, чем цилиндрические, коэффициентом перекрытия ε и меньшим числом зубьев z_min, которое может быть получено без подрезания.

Параметр ОР – называют внешним делительным конусным расстоянием

. (9)

b –ширина зубчатого венца принимается конструктивно:

.

Существуют рекомендация

.

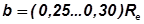Высота головки и высота ножки измеряются по образующим дополнительных конусов и назначаются

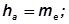
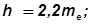
Определяем Θ_а – угол головки зуба и Θ_f – угол ножки зуба.

; . (10)

Углы конусов вершин и впадин соответственно равны

; . (11)

Геометрический расчет конической прямозубой передачи выполняется в соответствии ГОСТ 19624-74.

Рассмотренный вид колес имеет название октоидных конических колес. Получаются они при нарезании методом обкатки с помощью инструментальной плоскости (И.П.), жестко связанной с производящей плоскостью (П.П.), которая без скольжения катится по поверхности делительного конуса (а не основного). Поверхность, огибающая семейство инструментальных плоскостей в системе координат, связанной с делительным конусом, является боковой поверхностью зубьев октоидного конического колеса.

Практически в станках коническое колесо формируется с помощью плосковершинного производящего колеса, у которого угол конуса вершин равен 90˚. Зубья производящего колеса выполняются в виде двух резцов, каждый из которых нарезают одну из сторон зуба конического колеса (рис.4).

Рисунок 4 – Схема нарезания конического колеса

Резцы имеют прямобочный профиль и движутся прямолинейно к центру сферы О и вдоль высоты зуба.

Кроме этого резцам (резцовой головке) и заготовке сообщается относительное движение обкатки в соответствии с числом зубьев нарезаемого колеса.

Дата добавления: 2014-01-06