
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение логических задач
|
|
|
|
В ряде задач приводится несколько высказываний относительно некоторого события, и имеются некоторые сведения об их ложности или истинности. Требуется определить какое из событий имело место. Такие задачи называются логическими.
Алгоритм:
1. Вводятся обозначения для элементарных высказываний.
2. Записывают имеющиеся высказывания в виде формул логики высказываний со значениями равными 1 (при необходимости прибегаем к отрицанию).
3. Записываем конъюнкцию полученных формул и приравниваем её 1. (Характеристическое уравнение).
4. Приводим левую часть уравнения к ДНФ (СДНФ).
5. Каждый конъюнктивный член (независимо от других) приравниваем 1.
6. Решаем получившиеся уравнения. Каждое из решений характеристического уравнения является решением задачи.
Замечание. Можно строить формулы со значениями, равными 0. Тогда характеристическое уравнение получается как дизъюнкция этих формул, равная 0. Затем приводим к КНФ.
Задача:
В конкурсе участвовало 4 девушки: Оля, Нина, Марина и Тамара.
На вопрос о том, как распределились между ними места, были получено три ответа:
Оля ─ 1, Нина ─2,
Оля ─ 2, Тамара ─ 3,
Марина ─ 2, Тамара ─ 4.
Известно, что хотя бы одно высказывание в каждом ответе истинно. Как распределились места?
Решение:
Введем обозначения:
О
 Н
Н ; О
; О
 Т
Т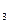 ; М
; М
 Т
Т .
.
Тогда КНФ: (О
 Н
Н  ) (О
) (О
 Т
Т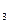 ) (М
) (М
 Т
Т  )
) 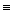 1, т.к. Каждое из элементарных сумм истинно.
1, т.к. Каждое из элементарных сумм истинно.
Преобразуем в ДНФ, раскрывая скобки:
(О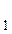
 Н
Н  ) (О
) (О М
М
 О
О Т
Т
 Т
Т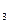 М
М
 Т
Т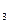 Т
Т  )
) 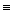
(т.к. О2 М 2 = 0 и Т3Т4 = 0) 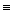 (О
(О
 Н
Н  ) (О
) (О Т
Т
 Т
Т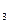 М
М  )
) 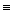 (раскрываем скобки)
(раскрываем скобки) 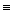
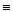 О
О О
О Т
Т
 О
О Т
Т М
М
 Н
Н О
О Т
Т
 Н
Н Т
Т М
М
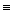
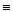 О
О Т
Т М
М .
.
Получили О Т
Т М
М
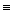 1.
1.
Следовательно: Оля ─ 1,Марина ─ 2, Тамара ─ 3, Нина ─ 4.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 286; Нарушение авторских прав?; Мы поможем в написании вашей работы!