Анализ рассуждений

Рассуждение ─ это вывод, позволяющий из данных высказываний (называемых посылками) получить новое высказывание (заключение).

Рассуждение состоит из последовательности посылок и заключения, то есть на основании известных свойств некоторых посылок мы получаем новое свойство этого объекта ─ заключение.

Рассуждение считается правильным, если из истинных посылок не может следовать ложного заключения.

Так как каждая посылка ─ это высказывание, то оно может быть записано в виде формулы. Следовательно, рассуждение – это последовательность формул. Заключение тоже является формулой.

Если 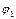, ,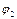…, 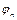-это последовательность посылок. а 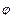─ заключение, то будем писать

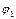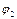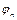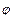, ,…, ├ или . (1)

И будем говорить, что из посылок логически следует заключение.

Нас будет интересовать только форма рассуждения, а не конкретное содержимое каждого высказывания, и на основании анализа формы мы будем делать вывод о том, правильное или неправильное рассматриваемое рассуждение. Если рассуждение признается правильным, то все рассуждения, приведенные по этой форме, правильны, независимо от того, к какой предметной области они относятся.

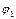
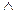
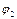
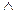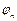
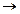
Теорема.Рассуждение (1) правильно тогда и только тогда, когда формула … 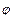– тавтология. (2)

Доказательство:

Достаточность:

Если (2 ) ─ это тавтология, то конъюнкция посылок не может быть равно 0, значит 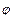=1, следовательно, рассуждение правильно.

Необходимость:

Если (1) правильно, то из истинности посылок 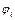не может следовать ложного заключения 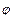. Это означает, что (2) не может обратиться в 0. Следовательно, (2 ) – тавтология.

Что и требовалось доказать.

Пример 1.

Пусть имеется рассуждение:

1. Если многоугольник правильный, то в него можно вписать окружность.

2. Данный многоугольник правильный.

3. Следовательно, в него можно вписать окружность.

Введем обозначения:

р ─ многоугольник правильный.

q ─ в многоугольник можно вписать окружность.

Посылки: 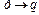, р. Заключение – q.

Рассуждение принимает вид: pq, р ├ q.

Формула, соответствующая этому рассуждению:

(pq) pq.

Установим вид этой формулы. Сняв импликацию, получим:

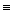(по законам де Моргана)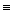 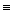(снимая двойное отрицание)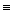 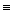(по второму закону дистрибутивности) 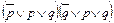. Это КНФ. Каждая элементарная сумма содержит высказывание со своим отрицанием, значит формула – тавтология.

Следовательно, рассуждение правильное.

Дата добавления: 2014-01-06