
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила вывода. Рассуждения, построенные по формуле (pq), будут правильными. Эта формула является тавтологией и называется правилом заключения (ПЗ).
|
|
|
|
Рассуждения, построенные по формуле (p q)
q) 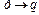 , будут правильными. Эта формула является тавтологией и называется правилом заключения (ПЗ).
, будут правильными. Эта формула является тавтологией и называется правилом заключения (ПЗ).
(p q) p
q) p q (ПЗ).
q (ПЗ).
Пример 2.
Пусть имеется рассуждение:
1. Если многоугольник правильный, то в него можно вписать окружность.
2. В многоугольник нельзя вписать окружность.
3. Следовательно, он неправильный.
Используя обозначения предыдущего примера, получим формулу, соответствующую этому рассуждению: (p q)
q) 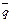
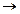
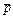 .
.
Аналогично предыдущему установим, что эта формула ─ тавтология, значит рассуждение правильное.
Данная формула называется правилом отрицания (ПО).
(p q)
q) 

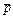 (ПО).
(ПО).
Пример 3.
Ппусть имеется рассуждение:
Если многоугольник правильный, то в него можно вписать окружность, следовательно, если в многоугольник нельзя вписать окружность, то он неправильный.
Рассуждение p q ├
q ├ 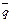
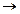
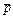 ─ правильное
─ правильное
Доказательство:
Соответствующая формула
(p q)
q)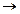 (
(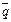
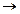
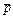 )
)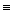 (
( )
)
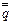

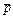
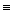 р
р 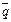
 q
q 

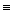 (р
(р q
q 

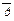 )(q
)(q 
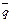

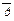 )
)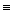 1, значит, рассуждение правильное.
1, значит, рассуждение правильное.
Данная формула называется правилом контрапозиции (ПК).
(p q)
q)  (
(

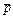 ) (ПК).
) (ПК).
Пример 4.
Пусть имеется рассуждение:
Если в треугольнике все стороны равны, то он равносторонний.
Если треугольник равносторонний, то его углы равны 60 , следовательно, если в треугольнике стороны равны, то углы по 60
, следовательно, если в треугольнике стороны равны, то углы по 60 .
.
Введем обозначения:
р ─ в треугольнике стороны равны.
q – треугольник равносторонний.
r – углы равны 60 .
.
Рассуждение: p q, q
q, q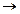 r ├ р
r ├ р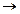 r.
r.
Соответствующая формула:
(p q)(q
q)(q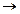 r)
r) 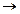 (р
(р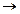 r)
r) 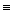 1 ─ рассуждение правильное.
1 ─ рассуждение правильное.
Данная формула называется правилом силлогизма (ПС).
(p q)(q
q)(q r)
r)  (р
(р r) (ПС).
r) (ПС).
Замечание. Формулы (ПЗ), (ПО), (ПК), (ПС) называются правилами вывода.
Правило вывода иногда записывают в виде:  .
.
ПЗ:  , ПО:
, ПО:  ,
,
ПК:  , ПС:
, ПС:  .
.
Другие правила вывода:
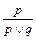 - введение дизъюнкции (ВД).
- введение дизъюнкции (ВД).
Доказательство. р 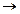 (р
(р  q)
q) 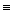
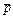
 р
р q
q 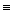 1.
1.
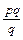 - удаление конъюнкции (УК).
- удаление конъюнкции (УК).
Доказательство. рq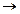 р
р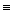

 р
р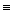
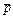

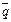
 р
р 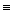 1.
1.
 - введение конъюнкции. (ВК)
- введение конъюнкции. (ВК)
Доказательство. рq 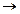 рq
рq 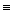 1
1
 удаление дизъюнкции (УД).
удаление дизъюнкции (УД).
Доказательство.

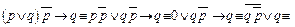

Существуют и другие правила вывода.
Замечание:
Так как правила вывода являются тавтологиями, то подстановка вместо элементарного высказывания любой формулы даст нам тавтологию, каждая из которых может быть объявлена правилом вывода.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 461; Нарушение авторских прав?; Мы поможем в написании вашей работы!