
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Префиксное кодирование
|
|
|
|
Кодирование с минимальной избыточностью
При равномерном кодировании общая длина кода зависит от длины сообщения. Возникает необходимость произвести неравномерное кодирование так, чтобы избыточность была минимальной.
Пусть задан алфавит А, и мы назначили неравномерные коды этому алфавиту. Например, букве А – 4 – битный код; Б – 6 – битный код; Ъ – 2 – битный код; О – 7 – битный код и так далее. Ясно, что в обычном тексте Ъ встречается реже буквы О, следовательно, если мы переназначим коды: О – 2 – битный код, Ъ – 7 – битный код, то общая длина кода уменьшится.
Алгоритм для сообщения S:
1) Находим частоту появления каждой буквы в заданном сообщении.
2) Элементарный код наименьшей длины ставим в соответствие букве с наибольшей частотой и так далее.
Замечание:
Это кодирование применимо для данного сообщения S. Для другого сообщения частота появления букв может быть другой, следовательно, элементарные коды могут быть другими.
Пусть имеется алфавит А. Таблица соответствия буквам алфавита А элементарных кодов, называется схемой кодирования.
Схема кодирования 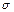 называется префиксной, если не один элементарный код не является префиксом другого элементарного кода.
называется префиксной, если не один элементарный код не является префиксом другого элементарного кода.
Например:
А ={ a,b }; B ={0,1};
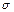 ={ а
={ а  0; b
0; b  01} – не префиксная схема.
01} – не префиксная схема.
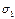 ={ a
={ a  0; b
0; b  10} - префиксная схема.
10} - префиксная схема.
Схема кодирования называется разделимой, если любой код однозначным образом разбивается на элементарные коды, то есть если код 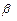 =
=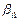 ,
,  ,…,
,…, 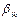 =
=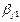 ,
, 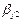 ,…,
,…, 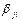 , то
, то 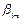 =
=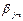 и k =
и k = , т.е. возможно однозначное декодирование.
, т.е. возможно однозначное декодирование.
Теорема. Префиксные схемы разделимы.
Доказательство:
Пусть схема 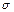 ={ αi
={ αi  βi }|
βi }|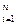 префиксная, но неразделима. Так как схема неразделима, то существует некоторое t такое, что
префиксная, но неразделима. Так как схема неразделима, то существует некоторое t такое, что 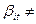
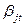 . А это значит, что есть такое
. А это значит, что есть такое  , что
, что 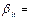
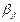
 или
или  =
=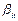
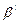 , то есть элементарный код
, то есть элементарный код 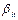 содержит
содержит  и
и 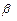
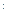 , а значит, является префиксом, следовательно, кодирование – не префиксное. Пришли к противоречию, означающее, что наше утверждение о неразделимости схемы неверно, следовательно, схема разделима.
, а значит, является префиксом, следовательно, кодирование – не префиксное. Пришли к противоречию, означающее, что наше утверждение о неразделимости схемы неверно, следовательно, схема разделима.
Что и требовалось доказать.
Замечание: утверждение о том, что из разделимости схемы следует её префиксносность, неверно.
Пример:
А ={ a, b }; B ={0, 1};
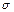 : { а
: { а  0; b
0; b  01} – схема не префиксная. Покажем, что она разделима.
01} – схема не префиксная. Покажем, что она разделима.
Сообщение: ab  001. Будем декодировать. Первая цифра 0 может быть кодом буквы а, а может быть префиксом буквы b. Но следующая цифра тоже 0. Значит, первый 0 не является префиксом буквы b, т.е. это код буквы а. Если предположить, что второй 0. это код буквы а, то следующий код начинается с 1, а таких кодов у нас нет, и мы вынуждены признать, что имеем код 01, т.е. букву b. Таким образом, получили 001
001. Будем декодировать. Первая цифра 0 может быть кодом буквы а, а может быть префиксом буквы b. Но следующая цифра тоже 0. Значит, первый 0 не является префиксом буквы b, т.е. это код буквы а. Если предположить, что второй 0. это код буквы а, то следующий код начинается с 1, а таких кодов у нас нет, и мы вынуждены признать, что имеем код 01, т.е. букву b. Таким образом, получили 001  ab.
ab.
Декодирование можно начать и с конца. Если последний символ 1, то рассмотрим предпоследний. Если он 0, то эти два символа соответствуют букве b. Если он 1, то кодирование произведено неверно. В нашем случае 01 соответствует b.
Исключаем из рассмотрения эти два символа. Следующий символ от конца 0. А 0 – это а. Если у нас есть еще символы – продолжаем.
Еще пример для той же схемы:
aabbaba  0001010010.
0001010010.
Первый символ 0. Это значит, что он может соответствовать а или являться префиксом b. Рассмотрим следующий. Если он 1, то первые два символа являются элементарным кодом b, но не а, т.к. с 1 код начинаться не может. После этого рассматриваем третий аналогично первому. Так как второй символ у нас 0, то первый символ – это элементарный код буквы а. Рассматриваем второй аналогично первому. И т.д.
Получим 0001010010  aabbaba.
aabbaba.
Замечание: кодирование произведено неверно, если код начинается с 1 или две 1 стоят подряд внутри кода.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 3773; Нарушение авторских прав?; Мы поможем в написании вашей работы!