Лемма 1

Оптимальное кодирование

При использовании кодирования по алгоритму Фано мы получаем некоторую цену кодирования. Так как разбиение на две части неоднозначно, то цена кодирования может меняться, то есть является некоторой функцией длины элементарных кодов. А так как эта цена кодирования конечна, то она имеет наименьшее значение. Кодирование, при котором цена кодирования имеет наименьшее значение, называется оптимальным. Т.к. число вариантов кодирования конечно, то оптимальное кодирование существует.

Таким образом, алгоритм Фано дает кодирование близкое к оптимальному.

Рассмотрим несколько вопросов, относящихся к оптимальному кодированию.

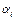
Пусть имеется распределение вероятностей p₁ ≥ p₂ ≥… ≥ p_n (1) и оптимальная схема кодирования ={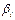}|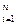. (2)

Тогда для любого j>i имеем: .

Доказательство:

Пусть существует такое j, что p_i > p_j, а 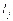<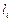. Тогда p_i 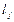< p_j .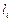

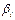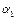
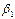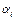
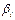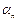
Взяв=, получим,что ={;…;…} и С < C , что противоречит оптимальности кодирования. Значит, наше предположение неверно и .

Лемма 2. Пусть имеется распределение вероятностей (1), и схема оптимального префиксного кодирования. Тогда среди кодов наибольшей длины есть два, которые отличаются друг от друга только последним разрядом.

Доказательство:

Допустим, что код максимальной длины один. По лемме 1: =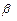0 или =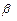1. Если 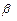─ префикс, то найдется такое j, что 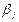=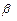. Это значит, что - префикс 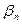. А это невозможно, так как кодирование префиксное. 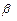─ не префикс, следовательно, оно может быть включено в схему кодирования:

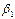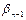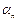
={;…;…}. Так как |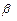|<, то p_{n ·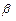} ||< p_{n ·} . Следовательно, С < C . А это противоречит оптимальности данной схемы кодирования.

Докажем теперь, что два кода наибольшей длины отличны только лишь в последнем разряде:

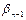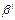
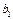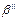
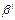
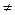
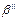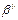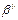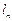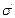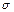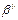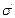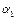
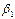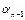
Пусть =, =, . Ни один из элементарных кодов не может быть префиксом , и, так как, он не префикс, то его можно выбрать в качестве элементарного кода: ||<.Тогда , совпадающая с до (n -1) кода, и в которой n – ый код равен Получим: ={;…,;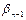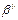}. Эта схема имеет цену кодирования С < C , так как |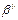| < 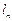. А это противоречит оптимальности. Значит наше предположение неверно и два кода наибольшей длины отличны только лишь в последнем разряде.

Дата добавления: 2014-01-06