
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема об оптимальном кодировании
|
|
|
|
Пусть имеется распределение вероятностей Р 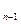 :
:
p1 ≥ p2 ≥… ≥ pn-1; 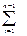 pi =1.
pi =1.
И пусть имеется префиксная схема оптимального кодирования:
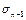 ={
={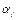

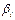 }|
}|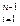 . (3) И пусть существует pj = q
. (3) И пусть существует pj = q + q
+ q , такое что pn-1≥ q1 ≥ q2. (4) Тогда схема кодирования:
, такое что pn-1≥ q1 ≥ q2. (4) Тогда схема кодирования: 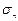 ={
={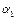

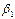 ;…;
;…; 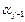

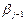 ;
; 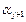

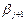 ;…;
;…; 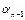

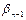 ;
; 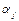

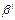 ;
; 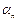

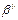 } (5)
} (5)
где 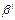 =
=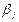 0,
0, 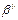 =
=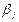 1, q1 соответствует
1, q1 соответствует 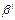 , q
, q  соответствует
соответствует 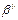 ,
,
является префиксной и оптимальной.
Разъяснение:
Эта теорема позволяет из оптимального кодирования алфавита, имеющего n- 1 букв, составить схему оптимального кодирования для другого алфавита, имеющего n букв, если выполнено условие (4). Смысл теоремы заключается в том, что для распределения вероятностей, состоящих из двух букв, мы можем произвести оптимальное кодирование. Например. р1 = 0,6 ─ код 0, р 2 = 0,4 ─ код 1.
Разобьем р 1: р 1 = 0,3 + 0,3. Каждое из слагаемых поместим в нижнюю часть распределения вероятностей, а имеющемуся коду первой буквы припишем 0 и 1. Получим оптимальную схему кодирования:.
р 1=0,4 код 1
р P2=0,3 код 00
р P3=0,3 код 01.
Далее, продолжая разбивать вероятность р 1 = 0,25 + 0,15, получим новую схему оптимального кодирования
р 1 = 0,3 00
р 2 = 0,3 01
р 3 = 0,25 10
р 4 = 0,15 11. и т.д.
Замечание:
Не всякая вероятность может быть разбита на два слагаемых, удовлетворяющих условию (4). Например: р 1 = 0,6; р 2 = 0,2; р 3 = 0,2;
р 1 не разбивается на два слагаемых, каждое из которых < 0,2.
Доказательство теоремы:
Схема кодирования (3) – префиксная. Цена кодирования
C 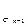 = р 1 l
= р 1 l  +…+ р n-1
+…+ р n-1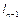 .
.
Схема (5) тоже будет префиксной по построению.
Цена кодирования
C 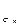 = р 1l
= р 1l  +…+ р j-1
+…+ р j-1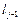 + р j+1
+ р j+1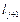 +…+ р n-1
+…+ р n-1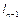 + q
+ q  |
|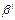 |+ q
|+ q  |
|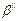 | =
| =
= р 1 l  +…+ р n-1
+…+ р n-1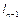 + q
+ q  (
(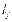 + 1) + q
+ 1) + q  (
(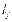 +1) =
+1) =
= р 1 l  +…+ р n-1
+…+ р n-1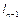 +
+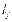 (q
(q + q
+ q ) + q
) + q +q
+q = р 1 l
= р 1 l  +…+ р n-1
+…+ р n-1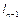 + +
+ + 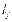 р j + p j = C
р j + p j = C 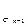 + pj.
+ pj.
Рассмотрим теперь схему оптимального кодирования
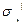 ={
={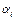

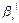 }|
}|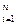 = {
= {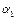

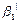 ;…;
;…; 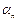

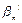 } (6)
} (6)
в которой 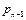 = q
= q  , р n = q
, р n = q  , pj = q
, pj = q + q
+ q .
.
По лемме 2: 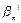 =
=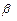 0,
0, 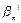 =
=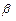 1.
1.
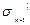 ={
={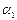

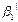 ;…;
;…;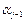

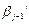 ;
;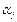

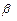 ;
;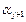

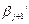 ;…;
;…; 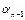

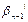 }, следовательно, C
}, следовательно, C 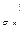 = C
= C 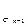 + pj (7) если pj = q
+ pj (7) если pj = q +q
+q . (8)
. (8)
Так как схема σ n-1 ─ схема оптимального кодирования, то
C 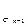
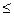 C
C 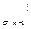 (9)
(9)
Получим C 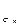 = C
= C 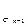 +
+ 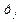 и в силу неравенства (9):
и в силу неравенства (9):
C 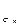 = C
= C 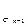 +
+ 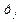
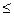 C
C 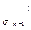 +
+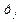 = C
= C 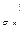 . Так как
. Так как 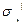 ─ оптимальна, то оптимальна и
─ оптимальна, то оптимальна и 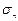 .Что и требовалось доказать.
.Что и требовалось доказать.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 621; Нарушение авторских прав?; Мы поможем в написании вашей работы!