Матрица инцидентности

Задание графа

Связность

Если для двух вершин существует цепь, то они называются связанными. Граф называется связным, если у него все вершины связны. Таким образом, если граф не связан. то из него можно выделить связные подграфы, называемые компонентами связности..

Рис. 35. Связный граф

Рис.36. Граф с двумя компонентами связности

1. Матрица смежности.

Пусть имеется граф G с n вершинами. Рассмотрим квадратную матрицу n ´ n, элементами которой являются 0 и 1.

а _ij =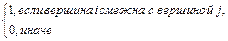

V V V… V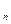

А =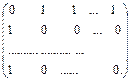

Эта матрица называется матрицей смежности, и она симметрична относительно главной диагонали.

Пример Дан граф

Матрица смежности

V V V V4

А =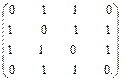

Рис. 37. Пример задания графа матрицей смежности

Матрица инцидентности устанавливает связь вершин и инцидентных с ней ребер.

b_ij =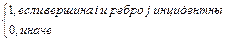

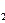Пример V l ₂ V

l ₁

l ₃

V1 V4

Матрица инцидентности

V V V V4

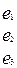
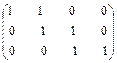
Рис.38. Задание графа матрицей инцидентности

4. Список смежности.

В списке смежности нужно указывать вершину и смежные с ней вершины.

V (V, V);

V (V, V);

V (V, V, V);

V (V, V);

V (V, V);

V (V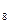, V, V);

V (V);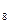

V (V);

Рис. 39. Задание графа списком смежности

Задание графа в виде списка смежности полезно при решении задачи обхода всех вершин графа: обследовать все вершины графа, побывав в каждой 1 раз.

Различают два метода решения этой задачи:

1) Поиск в глубину.

2) Поиск в ширину.

При поиске в глубину некоторая вершина выбирается в качестве начальной и помечается. Затем рассматривается список смежности этой вершины и из него выбирается первая вершина и помечается (какая-то вершина U). Рассматривается список смежности для вершины U. Выбирается первая вершина (W) и помечается. Рассматриваем список смежности для W, и так далее пока не столкнемся со случаем, что вершины списка помечены. Возвращаемся в вершину U и выбираем не помеченную вершину, если такая есть. Продвигаемся в этом направлении до тех пор, пока список вершины не оказывается помеченным. Опять возвращаемся назад и так далее. В итоге все вершины будут помечены.

Пример: См. рис. 39

Пусть начальная вершина ─ V (метка 1). В списке смежности вершины V числится V (метка 2). В списке смежности V─ вершина V (метка 3). В списке смежности вершины V имеются вершины V,V,V.

V уже помечена. Из V следуем в V (метка 5). VV (метка 6). Аналогично, VV( метка 7). Теперь возвращаемся в V. Все вершины помечены. Аналогично и в V,V, V. В списке смежности V имеется непомеченная вершина ─ V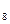 (метка 8). В списке V все вершины помечены. Возвращаемся в V. Здесь тоже все помечены. Следовательно, обход графа завершен. См. рис. 40

Рис. 40. Граф с помеченными вершинами при обходе в глубину

Приведенный нами алгоритм убеждает в справедливости теоремы:

Если граф конечен и связан, то при обходе в глубину каждая вершина обходится по одному разу.

Замечание:

Если при обходе в глубину (особенно для орграфов) оказывается ситуация, что при возращении в исходную вершину весь список помечен, но есть еще непомеченные вершины, то непомеченную вершину можно выбрать в качестве новой начальной и продолжить поиск.

Поиск в ширину. Смысл поиска в ширину заключается в том, что некоторую вершину V мы объявляем начальной ─ V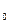. Перебираем весь список смежности этой вершины. Когда список исчерпан, т.е. все вершины, достижимые из V, помечены, мы переходим к первой вершине из помеченных. Затем, исчерпав список этой вершины, переходим ко второй вершине из первых помеченных и так далее до тех пор, пока не останется непомеченных вершин.

Пример: См. рис. 41.

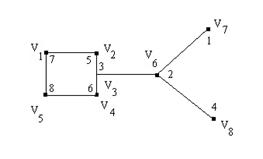Пусть V₇ (метка 1) ─ начальная вершина. В списке смежности у вершины V вершина V₆ (метка 2). Больше нет вершин в списке смежности V . Переходим в V . V (V, V, V ). Назначаем метку вершине V (метка 3). V ─ помечена, V (метка 4). Список вершины V исчерпан. Переходим в вершину V (V, V, V ). Вершины V (метка 5), V (метка 6). Возвращаемся в список вершины V . Вершины V и V 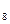─ помечены. Возвращаемся в V , и переходим затем в вершину V : V (V, V ). V (метка 7). Возвращаемся в V и переходим в V . V (V, V ). Переходим в V . Все вершины из списка V помечены. Переходим в V . Список V ─ помечен. Непомеченных вершин не осталось. Поиск в ширину закончен.

Рис 41. Метки вершин графа при поиске в ширину

Ясно, что последовательность поиска в глубину и в ширину зависит от выбора V.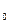

Дата добавления: 2014-01-06