
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема
|
|
|
|
Задача о наименьшем числе аварий
Пусть множество Х – множество печей для обжига кирпича, а множество У – множество платформ для сушки кирпича. Печи соединены с платформами рельсами. В месте пересечения рельсов вагонетки могут сойти с рельса. Ясно, чем меньше пересечений, тем меньше аварий. Каково наименьшее число аварий?
Поставим задачу в математическом виде.
Пусть имеется двудольный граф G 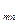 , где m и n – мощности множеств Х и У соответственно. Предположим, что вершины и ребра расположены в одной плоскости. В каждой точке, отличной от вершины пересекаются не более двух ребер. Оценим общее количество внутренних точек пересечения двудольного графа.
, где m и n – мощности множеств Х и У соответственно. Предположим, что вершины и ребра расположены в одной плоскости. В каждой точке, отличной от вершины пересекаются не более двух ребер. Оценим общее количество внутренних точек пересечения двудольного графа.
Введем обозначения: J (m, n) – функция, значением которой является число таких точек пересечения.
Нам известно, что граф Понтрягина – Куратоввского имеет не менее одного пересечения, т.е. J (3, 3) 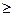 1.
1.
Справедлива
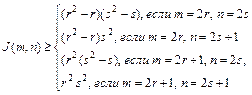
Доказательство:
На первом этапе докажем, что эта теорема справедлива при m = 3:
m = 3, значит r = 1, и тогда должно быть
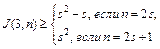
.Воспользуемся методом математической индукции:
Итак, положим s = 1.
Тогда
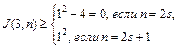 ,что справедливо. Граф (3,2) не имеет пересечений, в чем достаточно просто убедиться (рис. 42), а граф (3,3) - это граф Понтрягина – Куратоввского, имеющий одну точку пересечения.
,что справедливо. Граф (3,2) не имеет пересечений, в чем достаточно просто убедиться (рис. 42), а граф (3,3) - это граф Понтрягина – Куратоввского, имеющий одну точку пересечения.



 ● ● ●
● ● ●
 ● ●
● ●
Рис. 43. Двудольный граф (3,2)
Предположим, что теорема справедлива для некоторого s и докажем, что она справедлива для s + 1. Мы должны будем получить:
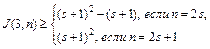 = =
= =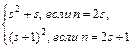 . (*)
. (*)
Разобьем граф G 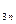 на подграфы.
на подграфы.
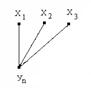
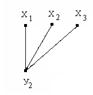
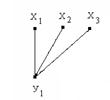
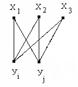 :
:
х1 х2 х33




 ● ● ●
● ● ●
● ●
yi yj
Рис. 44. Разбиение графа на подграфы и объединения их в пары
Будем рассматривать всевозможные пары этих подграфов
G  (i
(i 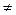 j):
j):
Может оказаться, что каждая пара имеет хотя бы одну точку пересечения. Общее число пар ─ число сочетаний Cn2. Тогда
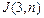 = Cn2 =
= Cn2 = 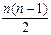 (1)
(1)
Полагая, что s = s +1, получим: если n ─ четное n = 2(S + 1) (2) и, если n – нечетное, то n = 2(s + 1) +1 (3)
Подставим формулу (2) в (1 ).
Получим:
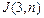 ≥
≥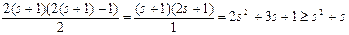 ,
,
что совпадает с оценкой (*).
Теперь подставим (3) в (1):
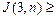
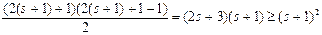 , что совпадает с оценкой (*).
, что совпадает с оценкой (*).
Предположим теперь, что имеется пара G  , не имеющая точек пересечения. Тогда у нас останется n - 2 подграфа, имеющих точки пересечения. По предположению индукции граф с (n - 2) вершинами должен иметь
, не имеющая точек пересечения. Тогда у нас останется n - 2 подграфа, имеющих точки пересечения. По предположению индукции граф с (n - 2) вершинами должен иметь 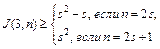 .
.
Добавим вершину n + 1:
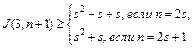 ,
,
что совпадает с оценкой (* ).
Мы доказали, что при m = 3 исходная формула справедлива.
Докажем теперь, что формула для оценки общих точек пересечения справедлива для любого m:
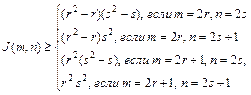 (4)
(4)
Воспользуемся методом индукции, т.е. докажем справедливость формулы (4) для
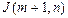 ,
, 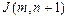 ,
, 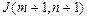 .
.
Рассмотрим первый случай.
При r= s = 1 формула справедлива.
Предположим, что m = 2r.
Разобьем граф G 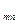 на подграфы и пронумеруем их:
на подграфы и пронумеруем их:
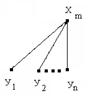
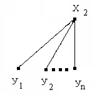
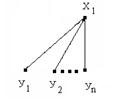
Рис. 45. Разбиение графа на подграфы
Объединим последовательно первый и второй, третий и четвертый и т.д.: (1, 2), (3, 4),…, (2 r -1, 2 r) подграфы. По индуктивному предположению формула (4 ) справедлива. Добавим х 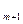 вершину. Эта вершина с каждой парой подграфов образует подграф G
вершину. Эта вершина с каждой парой подграфов образует подграф G 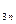 , а для него доказано, что число точек пересечения равно (s
, а для него доказано, что число точек пересечения равно (s 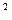 - s), если n =2 s, и s
- s), если n =2 s, и s 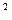 , если n = 2 s +1. Тогда общее число пересечений (у нас r пар)
, если n = 2 s +1. Тогда общее число пересечений (у нас r пар)
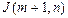 = J (m, n) + r (s
= J (m, n) + r (s 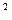 - s) или
- s) или 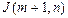 = J (m, n) + r s
= J (m, n) + r s 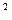 .
.
Получим:
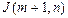 =(r
=(r 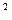 - r) (s
- r) (s 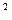 - s) + r (s
- s) + r (s 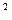 - s) = r
- s) = r 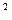 (s
(s 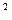 - s)
- s)
или
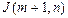 = (r
= (r 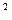 - r) s
- r) s 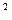 + rs
+ rs 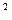 = r
= r 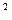 s
s 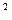 .
.
Таким образом, формула (4) справедлива.
Пусть теперь m = 2 r + 1 (нечетное).
Тогда при разбиении на пары подграфов последней вершине m – ой не хватает пары. Но если мы добавим (m + 1) - ую вершину, то получим подграф G 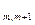 . Может оказаться, что этот подграф имеет точки пересечения или не имеет их. Если не имеет, то наша оценка не изменится, а если имеет, то только усилится.
. Может оказаться, что этот подграф имеет точки пересечения или не имеет их. Если не имеет, то наша оценка не изменится, а если имеет, то только усилится.
Если добавляется вершина во множество У, то доказательство ничем отличаться не будет. Если же вершина добавляется во множества Х и У, то сначала доказывается добавление во множество Х, а потом во множество У.
Что и требовалось доказать.
Пример: m = 4, n = 4, тогда r = 2, s = 2.
J (4, 4) 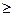 (2
(2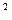 -2) (2
-2) (2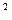 -2) = 4.
-2) = 4.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 342; Нарушение авторских прав?; Мы поможем в написании вашей работы!