Алгоритм Форда

Задача о кратчайшем пути

Взвешенный граф

Пусть задан граф G (V, E). Если каждому ребру этого графа поставлено в соответствие некоторое число, то граф называется взвешенным.

При задании взвешенных графов в матрицу смежности (или список) заносятся веса.

Пусть задан связный взвешенный граф. Будем истолковывать его вершины как населенные пункты, а веса как расстояния между ними. Поставим задачу о нахождении такого маршрута, соединяющего 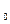х и х 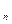, чтобй сумма расстояний была минимальной (маршрут не обязан включать все вершины).

	…
	…
		…

Рис. 46. Пример дорожного графа

Обозначим l ─ расстояние от i - той до смежной с ней j - той вершины. Задача о нахождении кратчайшего расстояния может быть решена прямым перебором всевозможных расстояний. Кроме кратчайшего расстояния нам необходимо еще и знание промежуточных вершин, через которые пролегает маршрут. Если n – велико, то эта задача становится трудно разрешимой. Возникает необходимость в разработке более компактного алгоритма.

Сущность этого алгоритма заключается в том, что каждой i - той вершине ставится в соответствие некоторое число 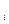, значение которого зависит от значения предыдущей вершины и расстояния между ними. Сначала объявляется 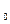= 0, а все остальные = ∞:

			…
	∞	∞	∞	∞

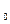
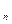
Обозначим через l расстояние между i - той и j - той вершинами.

Пусть назначена 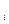i - той вершине (I = 0,1,…, n). Рассмотрим все j - ые вершины, смежные с i - той. Если 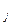- 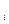> l (1)

то полагаем 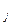=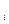+ l (2)

И так до тех пор, пока не дойдем до 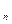. Значение 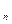и будет значением кратчайшего пути.

Обратный ход:

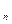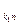Мы получили =+ l (1*)

Среди расстояний, соединяющих х 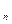со смежными вершинами, ищем l = -.

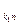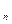Затем ищем вершину х 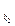, у которой =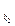+ l 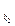. Затем переходим в х 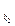и так далее, пока не доберемся до х .

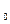Замечание 1:

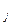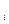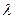
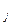Изменение значения происходит только тогда, когда выполняется неравенство (1), то есть >+ l . Заменяя значение по формуле (2 ), мы тем самым уменьшаем его. Так как граф связный, то висячих вершин нет, и, следовательно, каждая вершина получит значение .

Замечание 2:

При каждом поиске предыдущей вершины обратного хода необходимо проверять все смежные вершины, так как предыдущая вершина может быть не единственной.

Обоснование алгоритма:

Так как значение при каждом шаге может только уменьшаться, то последовательность значений для каждой вершины в конечном итоге принимает минимальное значение, т.е каждое - это кратчайшее расстояние данной вершины от х .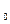

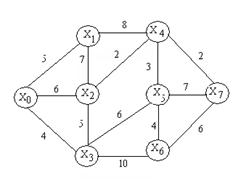Пример:

Рис. 47. Пример взвешенного графа

1) i = 0, j = 1, 2, 3;

J = 1: -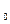= ∞ - 0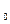 = 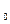∞ > l ; =+ l 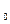= 5; заносим в таблицу.

j =2: -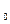= ∞ - 0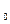 = 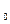∞ > l ; =+ l 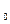= 6; заносим в таблицу.

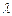
j =3: -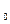= ∞ - 0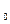 = 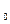∞ > l ; =+ l 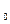= 4; заносим в таблицу.

2) i = 1, j = 0, 2, 4 (0 –уже не рассматриваем).

j = 2: -< 1₁ , <+ l ; значит не меняем

j = 4: >+ l , = 5 + 8 = 13; заносим в таблицу.

3) i = 2, j = 0, 1, 3, 4.

j = 0; не рассматриваем

j = 1: <+ l ; значит не меняем .

j = 3: <+ l ; значит не меняем

j = 4: >+ l , =6 +2 = 8; заносим в таблицу.

4) i = 3, j = 0, 2, 5, 6;

j = 0; не рассматриваем

j = 2: <+ l ; значит не меняем

j = 5: = 4+6 =10; заносим в таблицу.

j = 6: =+ l , = 4+ 10 =14; заносим в таблицу.

5) i = 4, j = 1,2,5,7;

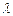
j = 1: <+ l ; значит не меняем

j =2: <+ l ; значит не меняем

j= 5: <+ l ; значит не меняем

j = 7: =+ l , = 10; заносим в таблицу.

6) i = 5, j = 3, 4, 6, 7;

j = 3: <+ l ; значит не меняем

j = 4: <+ l ; значит не меняем

j = 6: =+ , =14; заносим в таблицу.

j = 7: <+ l ; значит не меняем

7) i =6, j = 3, 5, 7;

j = 3: <+ l ; значит не меняем

j = 5: <+ l ; значит не меняем

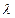
j = 7: <+ l ; значит не меняем

8) i = 7, j= 4, 5, 6;

j = 4; не рассматриваем

j = 5; не рассматриваем

j = 6: <+ l ; значит не меняем

Получили схему:

	∞	∞	∞	∞	∞	∞	∞
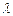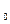
Итого

Обратный ход:

Начиная с последней вершины, проверяем все ей смежные на выполнение условия: l = -.

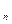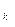Получим кратчайший путь хПоучаем: хххх.

Дата добавления: 2014-01-06