
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Связность в графах
|
|
|
|
Задача о максимальном потоке
Предварительно рассмотрим простую задачу.
Пусть трубопровод состоит из трех труб различного сечения с пропускными способностями 10 л/мин, 5 л/мин, 7 л/мин.
Вполне очевидно, что пропускная способность системы равна 5 л/мин, т.е. совпадает с наименьшей пропускной способностью труб.

10 л/мин 5 л/мин 7 л/мин
Рис. 48. Трубопровод
Пусть имеется некоторый взвешенный орграф G (V, E). Выделим в этом графе некоторые две вершины s, t, которые назовем источником и стоком.
Будем рассматривать веса как пропускную способность дуги q  . Количество фактически проходящих единиц по дуге обозначим через z
. Количество фактически проходящих единиц по дуге обозначим через z  . z
. z  - поток, проходящий через дугу i j. Ясно, что q
- поток, проходящий через дугу i j. Ясно, что q 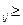 z
z  .
.
Пусть к источнику S прибывает поток Р. Для того, чтобы сеть функционировала нормально, должно быть Р  = Р
= Р 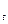 , Р
, Р 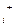 - Р
- Р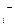 = 0. Требуется организовать перемещение так, чтобы величина Р была максимальной.
= 0. Требуется организовать перемещение так, чтобы величина Р была максимальной.
Разделим множество вершин на подмножества Х  и Х
и Х  . Рассмотрим дугу (V
. Рассмотрим дугу (V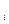 V
V 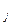 ) и отнесем вершину V
) и отнесем вершину V 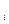 к Х
к Х 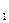 , а V
, а V 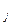 к Х
к Х  . Таким образом, для данного разбиения (Х
. Таким образом, для данного разбиения (Х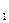 , Х
, Х  ) концы дуг принадлежат разным подмножествам. Такое разбиение называется разрезом, отделяющим вершину V
) концы дуг принадлежат разным подмножествам. Такое разбиение называется разрезом, отделяющим вершину V 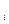 от V
от V 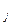 . Совокупность потоков, протекающих через Х
. Совокупность потоков, протекающих через Х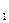 Х, называется потоком разреза.
Х, называется потоком разреза.
6.8.1. Теорема Форда – Фолкерсона
Теорема. Максимальный поток сети равен минимальному потоку разреза.
Доказательство:
Так как максимальный поток обязательно пройдет по дуге минимального разреза, то это будет означать, что он совпадает с минимальным потоком разреза. Это будет выполняться, если выполняется условия: Р  = Р
= Р 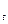 , т.е. Р
, т.е. Р  - Рt = 0.
- Рt = 0.
Предположим, что пропускные способности дуг выражаются целыми числами.
Будем последовательно строить разрезы, и назначать каждой вершине некоторое число – метку r по следующему правилу.
r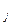 = min (r
= min (r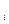 , q ij - z
, q ij - z  ), если z
), если z  ≤ q
≤ q  и дуга исходит из вершины V
и дуга исходит из вершины V 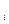 , и r
, и r 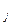 = z
= z  , при z
, при z  >0, если дуга заходит в V
>0, если дуга заходит в V 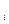 .
.
Для определенности в метку будем включать указатель вершины, из которой мы пришли в вершину V 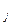 , то есть метка будет выглядеть: + V
, то есть метка будет выглядеть: + V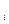 ,r
,r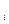 , если V
, если V 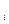 - вершина исхода; и - V
- вершина исхода; и - V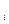 , r
, r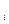 , если V
, если V 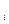 - вершина захода. Будем строить разрезы.
- вершина захода. Будем строить разрезы.
Включаем в разрез источник ─ вершину V 1, присвоив ей метку r  = ∞, и положив все потоки z
= ∞, и положив все потоки z  = 0.
= 0.
Просматриваем все смежные вершины, идущие в прямом направлении Γ+. Если им не присвоены метки, то присваиваем их
r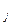 =min (r
=min (r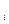 ,q
,q -z
-z  ) (1)
) (1)
Тем самым включаем эти вершины в подмножество Х1.
Просматриваем все смежные вершины, идущие в обратном направлении Γ-. Если им не присвоены метки, то присваиваем их
r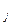 = z
= z > 0 (2).
> 0 (2).
Тем самым включаем эти вершины в подмножество Х1.
Проделаем это со следующей вершиной и со следующей, пока не дойдем до вершины t.
1). При этом, может оказаться, что вершина t попадает во множество Х 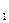 . Это будет означать, что полученные нами потоки могут быть увеличены на некоторую величину в для дуг в прямом направлении, и уменьшены в обратном направлении. Для полученной цепи, связывающей сток и источник (вершины меток) полагаем потоки равными меткам.
. Это будет означать, что полученные нами потоки могут быть увеличены на некоторую величину в для дуг в прямом направлении, и уменьшены в обратном направлении. Для полученной цепи, связывающей сток и источник (вершины меток) полагаем потоки равными меткам.
Для дуг, идущих в прямом направлении найдем b1 = min (q ij - z  ).
).
Для дуг, идущих в обратном направлении найдем b2 = min z > 0.
> 0.
Найдем b = min (b1, b2). Используя метки, строим цепь, связывающую сток с источником. Такие цепи называются аугментальными. Для дуг, идущих в прямом направлении, к имеющимся потокам прибавим величину b, и вычтем b из потоков в обратном направлении.
После этого стираем все метки и строим новые разрезы с новыми потоками.
2). Вершина t не попала в Х 1. Это значит, что для дуг в прямом направлении имеем q ij = z  , а для дуг в обратном направлении
, а для дуг в обратном направлении
z  .= 0. Иначе говоря, величина потока равна значению разреза, который и будет минимальным.
.= 0. Иначе говоря, величина потока равна значению разреза, который и будет минимальным.
Т.к. пропускные способности дуг выражаются целыми числами, то в случае 1) мы увеличивали поток на некоторое целое число, значит рано или поздно получим максимальный поток. Это наступит тогда, когда не останется аугментальных цепей.
Таким образом, установлено существование минимального разреза. Теорема доказана. Заодно, получен алгоритм нахождения наибольшего потока.
Пример.
Граф задается матрицей смежности (пропускных способностей дуг).
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | |
| V1 | ||||||||||
| V2 | ||||||||||
| V3 | ||||||||||
| V4 | ||||||||||
| V5 | ||||||||||
| V6 | ||||||||||
| V7 | ||||||||||
| V8 | ||||||||||
| V9 | ||||||||||
| V10 |
V2 V6 V8 V10








 ●
●



 V1 ● V4
V1 ● V4
 ● ● ●
● ● ●
V3 V5 V7 V9
Рис. 49. Пример сети с 10 вершинами
Вершина V 1 ─ источник, вершина V 10 ─ сток. Строим разрезы.
Вершине V 1присваиваем метку r 1= ∞, положив все потоки z  = 0.
= 0.
Просматриваем вершину V 1.
Γ+ (V 1) = { V2, V3 }.
Присваиваем вершине V 2 метку + V1, r2= min (r1,q12- z12) = = min (∞, 10 -0) =10. Метка V2: + V1, r2 = 10.
Присваиваем вершине V 3 метку + V1, r3= min (r1,q13- z13) = = min (∞, 17 -0) =17. Метка V3: + V1, r3 = 17.
Γ- (V 1) – пусто.
Вершина V 1 помечена и просмотрена.
Просматриваем вершину V 2.
Γ+ (V 2) = { V4, V6 }.
Присваиваем вершине V4 метку + V2, r4= min (r2, q24- z24) = min (10, 13 -0) =10. Метка V4: + V2, r 4 = 10.
Присваиваем вершине V6 метку + V2, r6= min (r2, q26- z26) = min (10, 23 -0) =10. Метка V6: + V2, r6 = 10.
Γ- (V2) = { V 1}. Но V1 помечена.
Вершина V2 помечена и просмотрена.
Просматриваем вершину V3.
Γ+ (V3) = { V4 }. Но V4 помечена.
Γ- (V3) = { V1, V5 }. Но V1 помечена, а z53 = 0..
Вершина V3 помечена и просмотрена.
Просматриваем вершину V4.
Γ+ (V4) = { V5 }.
Присваиваем вершине V5 метку + V4, r5= min (r4, q45- z45) = min (10, 5 -0) = 5. Метка V5: + V4, r5 = 5.
Γ- (V4) = { V2, V3 }. Но V2 помечена, и V3 помечена.
Вершина V4 помечена и просмотрена.
Просматриваем вершину V5.
Γ+ (V5) = { V7, V3 }.
Присваиваем вершине V7 метку + V5, r7= min (r5, q57- z57) = min( 5, 11 -0) = 5. Метка V7: + V5, r7 = 5.
Вершина V3 помечена.
Γ- (V5) – { V4, V6 }. Но V4 и V6 помечены.
Вершина V5 помечена и просмотрена.
Просматриваем вершину V6.
Γ+ (V6) = { V5, V7, V8 }. Но V5 и V7 помечены. Присваиваем вершине V8 метку + V6, r8= min (r6, q68- z68) = min (10, 21 -0) =10. Метка V8: + V6, r8 = 10.
Γ- (V6) = { V2 }. Но V2 помечена.
Вершина V6 помечена и просмотрена.
Просматриваем вершину V7.
Γ+ (V7) = { V9, V10 }.
Присваиваем вершине V9 метку + V7, r9= min (r7, q79- z79) = min (5, 8 - 0) =5. Метка V9: + V7, r9 = 5.
Присваиваем вершине V10 метку + V7, r10= min (r7, q710- z710) = min (5, 11 - 0) = 5. Метка V10: + V7, r10 = 5
Γ- (V7) = { V5, V6 V8 }. Но они помечены.
Вершина V7 помечена и просмотрена.
Все вершины помечены. Получили цепь V10, V7, V5, V4, V2, V1.
Назначим новые потоки, учитывая, что b= 5.
Метка V10: + V7, r10 = 5. Значит, поток z710 = 0 + 5 =5.
Метка V7: + V5, r7 = 5. Значит, поток z57 = 0 + 5 =5.
Метка V5: + V4, r 5 = 5. Значит, поток z45 = 0 + 5 =5..
Метка V4: + V2, r 4 = 10. Значит, поток z24 = 0 + 5 =5.
Метка V2: + V1, r2 = 10. Значит, поток z12 = 0 + 5 = 5.
Остальные потоки равны 0.
Стираем все метки и начинаем с начала строить разрезы с новыми потоками.
Вершине V1 присваиваем метку r1 = ∞.
Просматриваем вершину V1.
Γ+ (V1) = { V2, V3 }.
Присваиваем вершине V2 метку + V1, r2= min (r1, q12- z12) = min (∞, 10 -5) = 5. Метка V2: + V1, r2 = 5.
Присваиваем вершине V3 метку + V1, r3= min (r1, q13- z13) = min( ∞, 17 -0) = 17. Метка V3: + V1, r3 = 17.
Γ- (V1) – пусто.
Вершина V1 помечена и просмотрена.
Просматриваем вершину V2.
Γ+ (V2) = { V4, V6 }.
Присваиваем вершине V4 метку + V2, r4= min (r2, q24- z24) = min (5, 13 -5) = 5. Метка V4: + V2, r4 = 5.
Присваиваем вершине V6 метку + V2, r6= min (r2, q26- z26) = min (5, 23 -0) = 5. Метка V6: + V2, r6 = 5.
Γ- (V2) = { V1 }. Но V1 помечена.
Вершина V2 помечена и просмотрена.
Просматриваем вершину V3.
Γ+ (V3) = { V4 }. Но V4 помечена.
Γ- (V3) = { V1, V5 }. Но V1 помечена, а z53 = 0..
Вершина V3 помечена и просмотрена.
Просматриваем вершину V4.
Γ+ (V4) = { V5 }.
Присваиваем вершине V5 метку + V4, r5= min (r4, q45- z45) = min (5, 5 -5) = 0. Значит, этой вершине метку не присваиваем.
Γ- (V4) ={ V2, V3 }. Но V2 помечена, и V3 помечена.
Вершина V4 помечена и просмотрена.
Т.к. вершина V5 не помечена, то её пока не просматриваем.
Просматриваем вершину V6.
Γ+ (V6) = { V5, V7, V8 }.
Присваиваем вершине V5 метку + V6, r5= min (r6, q65- z65) = min (5, 14 - 0) = 5. Метка V5: + V6, r5 = 5.
.Присваиваем вершине V7 метку + V6, r7= min (r6, q67- z67) = min (5, 10 - 0) = 5 Метка V7: + V6, r7 = 5.
Присваиваем вершине V8 метку + V6, r8= min (r6, q68- z68) = min (5, 21 - 0) = 5. Метка V8: + V6, r8 = 5.
Γ- (V6) = { V2 }. Но V2 помечена.
Вершина V6 помечена и просмотрена.
Просматриваем вершину V5.
Γ+ (V5) = { V7, V3 }. Но V3 и V7 помечены.
Γ- (V5) – { V4, V6 }. Но V4 и V6 помечены.
Вершина V5 помечена и просмотрена.
Просматриваем вершину V7.
Γ+ (V7) = { V9, V10 }.
Присваиваем вершине V9 метку + V7, r9= min (r7, q79- z79) = min( 5, 8 - 0) =5. Метка V9: + V7, r9 = 5.
Присваиваем вершине V10 метку + V7, r10= min (r7, q710- z710)= min (5, 11 - 5) = 5.
Все вершины помечены.
Получили цепь V10, V7, V6, V2, V1.
Назначим новые потоки, учитывая, что b = 5.
Метка V10: + V7, r10 = 5. Значит, поток z710 = 5 + 5 = 10.
Метка V7: + V6, r7 = 5. Значит, поток z67 = 0 + 5 = 5.
Метка V6: + V2, r5 = 5. Значит, поток z26 = 0 + 5 = 5.
Метка V2: + V1, r2 = 10. Значит, поток z12 = 5 + 5 = 10.
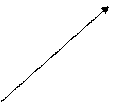
Потоки имеют вид
V2 5 V6 V8 V10



 ● ● ● ●
● ● ● ●
10 5
 V1 ● ● V4 5 10
V1 ● ● V4 5 10
 ● ● 5 ● ●
● ● 5 ● ●
V3 V5 V7 V9
Рис. 50. Распределение потоков после второй итерации
Стираем все метки и начинаем с начала строить разрезы с новыми потоками.
Вершине V1 присваиваем метку r1 = ∞.
Просматриваем вершину V1.
Γ+ (V1) = { V2, V3 }.
Присваиваем вершине V2 метку + V1, r2= min (r1, q12- z12) = min (∞, 10 - 10) = 0. значит, вершине V2 метка не присваивается.
Присваиваем вершине V3 метку + V1, r3= min (r1, q13- z13) = min (∞, 17 - 10) = 1. Метка V3: + V1, r3 = 17.
Γ- (V1) – пусто.
Вершина V1 помечена и просмотрена.
Т.к. вершина V2 не помечена, то её пока не просматриваем.
Просматриваем вершину V3.
Γ+ (V3) = { V4 }.
Присваиваем вершине V4 метку + V3, r4= min (r4, q34- z34) = min (17, 11 - 0) = 11. Метка V4: + V3, r4 = 11.
Γ- (V3) = { V1, V5 }. Но V1 помечена, а z53 = 0.
Вершина V3 помечена и просмотрена.
Просматриваем вершину V4.
Γ+ (V4) = { V5 }.
Присваиваем вершине V5 метку + V4, r5= min (r4, q45- z45) = min( 11, 5 - 5) = 0. Значит, этой вершине метку не присваиваем.
Γ- (V4) = { V2, V3 }. Но V3 помечена.
Присваиваем вершине V2 метку - V4, r2= z24 = 5.
Метка V2: - V4, r2 = 5.
Вершина V4 помечена и просмотрена.
Просматриваем вершину V2.
Γ+ (V2) = { V4, V6 }.
Но V4 помечена.
Присваиваем вершине V6 метку + V2, r6= min (r2, q26- z26) =
min (5, 23 - 5) = 5. Метка V6: + V2, r6 = 5.
Γ- (V2) = { V1 }. Но V1 помечена.
Вершина V2 помечена и просмотрена.
Т.к. вершина V5 не помечена, то её пока не просматриваем.
Просматриваем вершину V6.
Γ+ (V6) = { V5, V7, V8 }.
Присваиваем вершине V5 метку + V6, r5= min (r6, q65- z65) = min (5, 14 - 5) = 5.
Метка V5: + V6, r5 = 5.
Присваиваем вершине V7 метку + V6, r7= min (r6, q67- z67) = min (5, 10 - 5) = 5. Метка V7: + V6, r7 = 5.
Присваиваем вершине V8 метку + V6, r8= min (r6, q68- z68) = min (5, 21 - 0) = 5. Метка V8: + V6, r8 = 5.
Γ- (V6) = { V2 }. Но V2 помечена.
Вершина V6 помечена и просмотрена.
Просматриваем вершину V5.
Γ+ (V5) = { V7, V3 }. Но V3 и V7 помечены.
Γ- (V5) = { V4, V6 }. Но V4 и V6 помечены.
Вершина V5 помечена и просмотрена.
Просматриваем вершину V7.
Γ+ (V7) = { V9, V10 }.
Присваиваем вершине V9 метку + V7, r9= min (r7, q79- z79) = min (5, 8 - 0) = 5. Метка V9: + V7, r9 = 5.
Присваиваем вершине V10 метку + V7, r10= min (r7, q710- z710) = min (5,11- 10) = 1.
Γ- (V7) = { V5, V6 }. Но V4 и V6 помечены.
Все вершины помечены.
Получили цепь V10, V7, V6, V2, V4, V3, V1.
Имеем b1 = 1, b2 = 5. Тогда b = min (b1,b2) = 1.
Назначим новые потоки, учитывая, что b = 1.
Метка V10: + V7, r10 = 5. Значит, поток z710 = 10 + 1 = 11.
Метка V7: + V6, r7 = 5. Значит, поток z67 = 5 + 1 = 6.
Метка V6: + V2, r5 = 5. Значит, поток z26 = 5 + 1 = 6.
Метка V2: - V4, r2 = 5. Значит, поток z24 = 5 - 1= 4.
Метка V4: + V3, r4 = 11. Значит, поток z34 = 0 + 1 = 1.
Метка V3: + V1, r3 = 17. Значит, поток z13 = 0 + 1 = 1.
Потоки имеют вид
V6
 V2 6 V8 V10
V2 6 V8 V10
10 6
V1 4
 V4
V4
1 5 11
 1 5
1 5
V3 V5 V7 V9
Рис. 51. Распределение потоков после третьей итерации
Стираем все метки и начинаем с начала строить разрезы с новыми потоками.
Вершине V1 присваиваем метку r1 = ∞.
Просматриваем вершину V1.
Γ+ (V1) = { V2, V3 }.
Присваиваем вершине V2 метку + V1, r2 = min (r1, q12- z12) = min (∞,10 - 10) = 0. Значит, вершине V2 метка не присваивается.
Присваиваем вершине V3 метку + V1, r3= min (r1, q13- z13) = min (∞, 17 - 1) = 16. Метка V3: + V1, r3 = 16.
Γ- (V1) – пусто.
Вершина V1 помечена и просмотрена.
Т.к. вершина V2 не помечена, то её пока не просматриваем.
Просматриваем вершину V3.
Γ+ (V3) = { V4 }.
Присваиваем вершине V4 метку + V3, r4= min (r4, q34- z34) = min (17, 11 - 1) = 10. Метка V4: + V3, r4 = 10.
Γ- (V3) = { V1, V5 }. Но V1 помечена, а z53 = 0.
Вершина V3 помечена и просмотрена.
Просматриваем вершину V4.
Γ+ (V4) = { V5 }.
Присваиваем вершине V5 метку + V4, r5= min (r4, q45- z45) = min (11, 5 - 5) = 0. Значит, этой вершине метку не присваиваем.
Γ- (V4) ={ V2, V3 }. Но V3 помечена.
Присваиваем вершине V2 метку - V4, r2= z24 = 4.
Метка V2: - V4, r2 = 4.
Вершина V4 помечена и просмотрена.
Просматриваем вершину V2.
Γ+ (V2) = { V4, V6 }.
Но V4 помечена.
Присваиваем вершине V6 метку + V2, r6= min (r2, q26- z26) =
min (4, 23 - 6) = 4 Метка V6: + V2, r6 = 4.
Γ- (V2) = { V1 }. Но V1 помечена.
Вершина V2 помечена и просмотрена.
Т.к. вершина V5 не помечена, то её пока не просматриваем.
Просматриваем вершину V6.
Γ+ (V6) = { V5, V7, V8 }.
Присваиваем вершине V5 метку + V6, r5= min (r6, q65- z65) = =min (6, 14 - 6) = 6. Метка V5: + V6, r5 = 6.
Присваиваем вершине V7 метку + V6, r7= min (r6, q67- z67) =
min (6, 10- 6) = 4. Метка V7: + V6, r7 = 4.
Присваиваем вершине V8 метку + V6, r8= min (r6, q68- z68) = min (6, 21 - 0) = 6. Метка V8: + V6, r8 = 6.
Γ- (V6) = { V2 }. Но V2 помечена.
Вершина V6 помечена и просмотрена.
Просматриваем вершину V5.
Γ+ (V5) = { V7, V3 }. Но V3 и V7 помечены.
Γ- (V5) = { V4, V6 }. Но V4 и V6 помечены.
Вершина V5 помечена и просмотрена.
Просматриваем вершину V7.
Γ+ (V7) = { V9, V10 }.
Присваиваем вершине V9 метку + V7, r9= min (r7, q79- z79) = min (4, 8 - 0) = 4. Метка V9: + V7, r9 = 4.
Присваиваем вершине V10 метку + V7, r10= min (r7, q710- z710) = min (4, 11- 11) = 0. Значит, вершине V10 метка не присваивается.
Γ- (V7) = { V5, V8, V6 }. Но V5, V8 и V6 помечены.
Вершина V7 помечена и просмотрена.
Просматриваем вершину V8.
Γ+ (V8) = { V7 } Вершина V7 помечена.
Γ- (V8) = { V6, V10 }. Но V6 помечен, а z10 8 = 0.
Вершина V8 помечена и просмотрена.
Просматриваем вершину V9.
Γ+ (V9) = { V10 }.
Присваиваем вершине V10 метку + V9, r10= min (r9, q910- z910) = min (4, 23 - 0) = 4. Метка V10: + V9, r10 = 4.
Все вершины помечены.
Получили цепь V10, V9,V7, V6, V2, V4, V3, V1.
Имеем b1 = 4, b 2 =4. Тогда b = min (b 1, b 2) = 4.
Назначим новые потоки, учитывая, что b = 4.
Метка V10: + V9, r10 = 4. Значит, поток z910 = 0 + 4 = 4.
Метка V9: + V7, r9 = 4. Значит, поток z79 = 0 + 4 = 4.
Метка V7: + V6, r7 = 5. Значит, поток z67 = 6 + 4 = 10.
Метка V6: + V2, r5 = 5. Значит, поток z26 = 6 + 4 = 10.
Метка V2: - V4, r2 = 5. Значит, поток z24 = 4 – 4 = 0.
Метка V4: + V3, r4 = 11. Значит, поток z34 = 1 + 4 = 5.
Метка V3: + V1, r3 = 17. Значит поток z13 = 1 + 4 = 5.
Потоки имеют вид
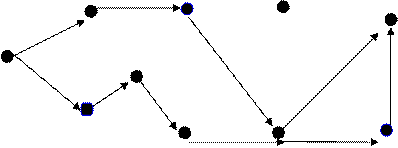 V2 10 V6 V8 V10
V2 10 V6 V8 V10
V1
10 11 4
5 5 V4
V3 5
V5 5 4 V9
V7 

Рис. 52. Распределение потоков после четвертой итерации
Стираем все метки и начинаем вновь строить разрезы с новыми потоками.
Вершине V1 присваиваем метку r1 = ∞.
Просматриваем вершину V1.
Γ+ (V1) = { V2, V3 }.
Присваиваем вершине V2 метку + V1, r2= min (r1, q12- z12) = min (∞, 10 – 10) = 0. Значит, вершине V2 метка не присваивается.
Присваиваем вершине V3 метку + V1, r3= min (r1, q13- z13) = min (∞, 17 - 5) = 12.
Метка V3: + V1, r3 = 12.
Γ- (V1) – пусто.
Вершина V1 помечена и просмотрена.
Т.к. вершина V2 не помечена, то её пока не просматриваем.
Просматриваем вершину V3.
Γ+ (V3) = { V4 }.
Присваиваем вершине V4 метку + V3, r4= min (r4, q34- z34) = min (12, 11 - 5) = 6.
Метка V4: + V3, r4 = 6.
Γ- (V3) = { V1, V5 }. Но V1 помечена, а z53 = 0.
Вершина V3 помечена и просмотрена.
Просматриваем вершину V4.
Γ+ (V4) = { V5 }.
Присваиваем вершине V5 метку + V4, r5= min (r4, q45- z45) = min (11, 5 - 5) = 0. Значит, этой вершине метку не присваиваем.
Γ- (V4) ={ V2, V3 }. Но V3 помечена, а z24 = 0.
Вершина V4 помечена и просмотрена.
Дальнейшая расстановка меток невозможна. Значит, полученный поток является оптимальным. Он равен 15.
Пусть задан граф G, у которого р – вершин и q – ребер. Если для двух вершин существует цепь, то они называются связными. Граф называется связным, если у него все вершины связны. Если граф может быть задан в виде объединения нескольких подграфов, то каждый такой подграф называется компонентой связности, а количество компонент обозначается буквой k.
Рис. 53. G = G1 U G2, k =2
 |
●
Рис. 54. Несвязный граф, k =3
Теорема. Пусть имеется три инварианта: р, q и k. Тогда
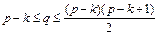
.
Доказательство по индукции:
1) Докажем, что р – k 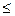 q (1)
q (1)
а). Пусть р = 1; q = 0; тогда k= 1 и р – k = 1- 1 = 0 = q ─ верно.
б). Пусть р = 2.
При k = 2, получим q = 0 и р – k = 0 = q. При k = 1: получим q= 1 и р – k = 1 = q.
Слдовательно, неравенство (1) справедливо.
в). Пусть неравенство (1 ) справедливо для некоторого р. Покажем, что оно справедливо и для р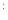 = р + 1, то есть мы должны показать, что справедливо р
= р + 1, то есть мы должны показать, что справедливо р -k
-k
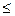 q
q  (2) где q
(2) где q  - количество ребер, получившихся после добавления вершины, а k
- количество ребер, получившихся после добавления вершины, а k  - число компонент нового графа.
- число компонент нового графа.
В самом деле:
При р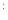 = р+ 1, k
= р+ 1, k = k + 1 и q
= k + 1 и q  = q получим р
= q получим р  - k
- k  = р + 1- k - 1 = р- k
= р + 1- k - 1 = р- k 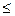 (в силу неравенства (1) )
(в силу неравенства (1) ) 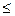 q = q
q = q  .
.
Если же при р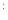 = р + 1 имеем q
= р + 1 имеем q = q + n (n
= q + n (n 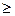 1) и k
1) и k = k, то р
= k, то р - k
- k = р+ 1 - k
= р+ 1 - k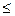 (в силу неравенства (1))
(в силу неравенства (1))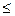 q + 1
q + 1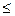 q+ n= q
q+ n= q .
.
Неравенство (2) доказано.
2) Докажем, что 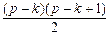
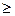 q (3)
q (3)
а). Пусть р = 1; q = 0; k = 1. Тогда 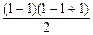 = 0 = q.
= 0 = q.
Пусть неравенство (3) справедливо для некоторого р. Докажем, что оно справедливо и для р = р + 1, т.е.
= р + 1, т.е.

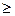 q
q  (4)
(4)
б). Пусть р = р + 1; q
= р + 1; q = q и k
= q и k =k + 1. (*)
=k + 1. (*)
Тогда
 =
= 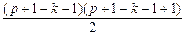 = =
= = 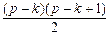
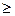 q = q
q = q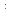
в). Пусть р = р + 1; q
= р + 1; q = q + 1 и k
= q + 1 и k =k. Тогда
=k. Тогда
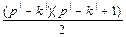 =
= 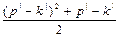 = (подставляя (*)
= (подставляя (*)
и раскрывая скобки) = 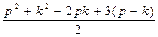
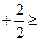
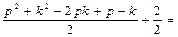
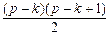 +1
+1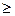 (в силу неравенства (3))
(в силу неравенства (3)) 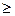 q + 1= q
q + 1= q  .
.
Что и требовалось доказать.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 480; Нарушение авторских прав?; Мы поможем в написании вашей работы!