Ответ. 0,07

Задание B10 (№ 320481) Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 4 раз попал в мишени, а последний раз промахнулся. Результат округлите до сотых.

Определение. Два события называются независимыми, если вероятность одного из них не изменяется в результате того, наступило или не наступило другое.

Примерами независимых событий являются выпадение различного числа очков при повторном бросании игральной кости или той или иной стороны монет при повторном бросании монеты, так как очевидно, что вероятность выпадения герба при втором бросании равна ½ независимо от того, выпал или не выпал герб в первом.

Аналогично, вероятность вынуть во второй раз белый шар из урны с белыми и черными шарами, если вынутый первым шар предварительно возвращен, не зависит от того, белый или черный шар был вынут в первый раз. Поэтому результаты первого и второго вынимания независимы между собой. Наоборот, если шар, вынутый первым, не возвращается в урну, то результат второго вынимания зависит от первого, ибо состав шаров, находящихся в урне после первого вынимания, меняется в зависимости от его исхода. Здесь мы имеем пример зависимых событий.

Теорема (о вероятности совместного осуществления двух независимых событий). Если события A и B независимы, то вероятность их пересечения равна произведению вероятности этих событий: P(AÇB)=P(A)·P(B).

Рассмотрим теперь несколько событий: A, B, …, L. Будем называть их независимыми в совокупности, если вероятность появления любого из них не зависит от того, произошли ли какие – либо другие рассматриваемые события или нет.

Замечание. Отметим, что, из по парной независимости событий не следует их независимость в совокупности. В самом деле, рассмотрим пример.

Пусть в ящике 4 шара: черный, красный, белый и пестрый – окрашенный в полоску всеми этими тремя цветами. Обозначим события: после изъятия шара видим

A – “черный цвет”, B – “красный цвет”, C – “белый цвет”, тогда P(A)=P(B)=P(C)=1/2;

P_B(A)=P_C(A)=P_A(C)=P_B(C)=P_C(B)=P_A(B)=1/2.

Отсюда

P_B(A)=P(A); P_C(A)=P(A); P_A(C)=P(C); P_B(C)=P(C); P_C(B)=P(B); P_A(B)=P(B).

Это значит, что события A, B, C попарно независимы. Тем не менее, если известно, что в результате изъятия шара наступили события A и B, то вероятность события C становится равной 1. Значит, в совокупности A, B и C не являются независимыми.

Теорема (о вероятности совместного осуществления событий независимых в совокупности). Вероятность пересечения событий A, B, …, L независимых в совокупности, равна произведению вероятностей этих событий: P(AÇBÇ…ÇL)=P(A)·P(B)·…·P(L).

Решение. Итак, представим биатлониста стреляющего по мишеням расположенным в 500 метрах от места ведения огня. Биатлонист делает первый выстрел. Как вы думаете, важен ли результат одного выстрела? Если важен, то биатлонист поднимается, пробегает каких-то 500 метров до мишеней, возвращается обратно и делает второй выстрел. Как вы считаете, важен ли результат двух выстрелов? Если важен, то биатлонист снова поднимается, добегает до мишеней и, реально, видит результаты двух выстрелов, в том числе и первого. Возвращается на линию огня и делает третий, четвертый и пятый выстрелы. После чего он добегает до мишеней и смотрит результат всех пяти выстрелов. Давайте подумаем, чем может отличаться один такой результат от другого? Действительно, первое – количеством попаданий и промахов, второе – порядком попаданий и промахов. А значит результатами (исходами) его стрельбы могут быть:

U₁={П; П; П; П; П}, здесь и далее П – попал при одном выстреле, Н – не попал при одном выстреле,

U₂={П; П; П; П; Н}, U₃={П; П; П; Н; Н}, U₄={П; П; Н; Н; Н}, U₅={П; Н; Н; Н; Н}, U₆={Н; Н; Н; Н; Н}, U₇={Н; П; П; П; П}, U₈={Н; Н; П; П; П}, U₉={Н; Н; Н; П; П}, U₁₀={Н; Н; Н; Н; П}, U₁₁={Н; П; Н; Н; Н}, U₁₂={Н; П; П; Н; Н}, U₁₃={Н; П; П; П; Н}, U₁₄={Н; П; Н; П; Н}, U₁₅={Н; Н; П; Н; Н}.

Споткнувшись о техническую трудность, связанную с выписыванием всех возможных исходов, возникают вопросы: «Насколько это необходимо для решения поставленной задачи? Нельзя ли ограничиться рассмотрением лишь «нужных» для решения этой задачи исходов?» Событию A - «биатлонист первые 4 раза попал в мишени, а последний раз промахнулся», вероятность которого требуется найти, благоприятствует лишь один исход U₂={П; П; П; П; Н}. Вероятность этого исхода, а стало быть, и искомая вероятность, согласно теореме о вероятности совместного осуществления событий независимых в совокупности, равна произведению, то есть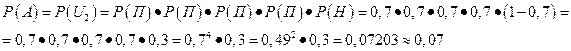

12. Задание B10 (№ 322293) Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Протор» по очереди играет с командами «Стратор», «Стартер» и «Ротор». Найдите вероятность того, что «Протор» будет начинать только вторую и последнюю игры.

Решение. Согласно условию задачи, команда «Протор» по очереди играет с каждой из трёх команд «Стратор», «Стартер» и «Ротор», то есть суждено случиться трём играм: «Протор» - «Стратор», «Протор» - «Стартер» и «Протор» - «Ротор». А значит, для того чтобы определиться какая из команд в каждой игре начнет игру с мячом, капитану команды «Протор» придётся три раза тянуть честный жребий. Поэтому возможными исходами рассматриваемого опыта служат:

U₁={П+; П+; П-}, здесь и далее П+ – команда «Протор» начинает игру с мячом, П- – игру с мячом начинает противник команды «Протор», U₂={П+; П+; П+}, U₃={П+; П-; П-}, U₄={П-; П+; П+}, U₅={П-; П-; П+}, U₆={П-; П-; П-}, U₇={П-; П+; П-}, U₈={П+; П-; П+}. Таким образом, множество всевозможных исходов рассматриваемого опыта состоит из восьми элементов U₁, U₂, U₃ ,… U₇, U₈. Эти исходы взаимно исключают друг друга, и в результате опыта один из них обязательно произойдет. Событию D – «команда «Протор» начнёт вторую и последнюю игры» благоприятствует исход U₄, а значит искомая вероятность равна вероятности этого исхода U₄={П-; П+; П+}. Поскольку, возможность вытащить жребий с правом начала игры, не обладает ни каким преимуществом перед возможностью не вытащить такой жребий, то 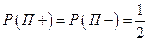. А значит искомая вероятность, согласно теореме о произведении вероятностей событий независимых в совокупности, равна произведению: .

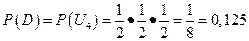Дата добавления: 2014-01-06