Ответ. 0,168

Задание B10 (№ 319553) Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,56. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Ответ. 0,019.

Замечание. Можно воспользоваться теоремой о полной вероятности, возможно, это сократит время решения. Но с точки зрения понимания... Не уверен!!!

Решение. Опыт состоит в проведении двух шахматных партий гроссмейстером A. По условию задачи известно, что одну из двух партий гроссмейстер A однозначно играет белыми фигурами, а вторую партию – однозначно чёрными, именно поэтому вероятность выигрыша гроссмейстера A в одной из партий равна 0,56, а вероятность его же выигрыша в другой партии равна 0,3. А значит, искомая вероятность, по теореме о вероятности совместного осуществления независимых событий, равна произведению 0,56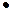0,3 и равна 0,168.

Отметим, что возможными исходами рассматриваемого опыта являются: U₁={А_б+; А_ч-}, здесь и далее А_б+ означает, что гроссмейстер А играл белыми фигурами и выиграл, А_ч- означает, что гроссмейстер А играл черными фигурами и проиграл, то есть выиграл гроссмейстер Б, U₂={А_б+; А_ч+}, U₃={А_б-; А_ч+}, U₄={А_б-; А_ч-}. Таким образом, множество всех исходов рассматриваемого опыта состоит из четырёх элементов. Нетрудно найти, что P(U₁)=0,56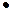0,7=0,392, P(U₂)=0,56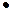0,3=0,168, P(U₃)=0,44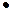0,3=0,132 и P(U₄)=0,440,7=0,308. Поскольку, P(U₁)+P(U₂)+P(U₃)+P(U₄)=0,392+0,168+0,132+0,308=1, то можно предположить, что, скорее всего, задача решена правильно и все возможные исходы учтены.

Дата добавления: 2014-01-06