Показательное распределение. Плотность вероятности и функция распределениядля показательного распределения имеют вид

Плотность вероятности и функция распределениядля показательного распределения имеют вид

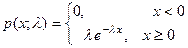
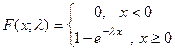
Построим графики плотности вероятности и функции распределения для значений (сплошной линией) и 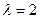(пунктирной линией)

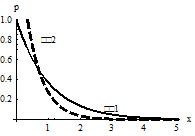
Плотность вероятности Функция распределения

Среди непрерывных распределений только показательное распределение обладает свойством отсутствия последействия.

Действительно, пусть элемент, время безотказной работы которого распределено по показательному закону, проработал время 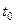. Тогда для вероятности времени безотказной работы .

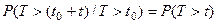Действительно,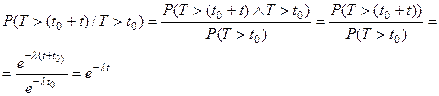

Распределение остатка времени безотказной работы не зависит от того, сколько времени прибор проработал. Предварительное использование элемента не влияет на оставшееся время его работы, т.е. у элемента нет старения. Показательное распределение используется в качестве модели времени безотказной работы сложной системы, элементы которой восстанавливаются в процессе работы..

По показательному закону распределена длительность работы многих приборов. Вероятность отказа прибора за время равна 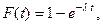вероятность безотказной работы прибора за время называется функцией надежности .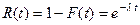

5. Закон Вейбулла.

Обобщением показательного распределения и распределения Релея является распределение Вейбулла, для которого плотность вероятности и функция распределения имеют следующее представление.

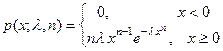
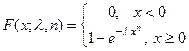
где ,

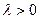
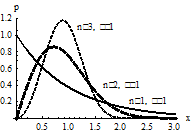
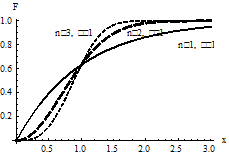
Плотность вероятности Функция распределения

При 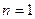закон Вейбулла становится показательным распределением, а при – распределением Релея. На рис приведены графики плотности вероятности и функции распределения в случае для 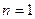(сплошной линией), для (пунктирной линией с длинными штрихами), для 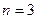(пунктирной линией с короткими штрихами).

Дата добавления: 2014-01-06