Метод Эйлера. В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, этот метод называется также методом ломаных Эйлера

В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, этот метод называется также методом ломаных Эйлера.

Угловой коэффициент касательной к интегральной кривой в точке M₀(x₀,y₀) равен .

Найдем ординату y₁ касательной, соответствующей абсциссе x₁=x₀+h.

Уравнение касательной к кривой в точке M₀ имеет вид или 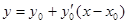, откуда y₁=y₀+hf(x₀,y₀).

Аналогично, угловой коэффициент касательной к интегральной кривой в точке M₁(x₁,y₁) равен 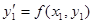. Точку M₂(x₂,y₂) получим соответственно

x₂=x₁+h y₂=y₁+hf(x₁,y₁).

Продолжая вычисления по данной схеме, получим формулы Эйлера для приближенного решения задачи Коши с начальными данными (x₀,y₀) на сетке отрезка [ a, b ] с шагом h:

x_i=x_i-1+h y_i=y_i-1+hf(x_i-1,y_i-1). (4)

M₄

M₃

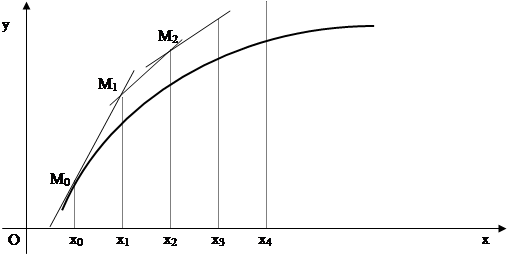
Графической иллюстрацией приближенного решения является ломаная, соединяющая последовательно точки M₀, M₁, …,M_m, которую называют ломаной Эйлера.

Погрешность метода Эйлера можно оценить неравенством

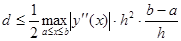, (5)

которое можно представить в виде d=Ch, где . Таким образом, метод Эйлера имеет первый порядок точности.

Практическую оценку погрешности решения, найденного на сетке с шагом h/2, в точке x_i Î[ a, b ] производят с помощью приближенного равенства – правила Рунге:

(6)

где P – порядок точности численного метода.

Таким образом, оценка полученного результата по правилу Рунге вынуждает проводить вычисления дважды: с шагом h и h/2, причем совпадение десятичных знаков в полученных двумя способами результатах дает основание считать их верными.

Программа решения дифференциального уравнения методом Эйлера

program Eiler;

var x,a,b,h,y:real;

m,i:integer;

function f(x,y: real): real;

begin f:=cos(x);

end;

begin writeln('Введите значения концов отрезка [a,b]');

readln(a,b);

writeln('Введите начальное значение y0=y(x0)');readln(y);

writeln('Введите число значений функции на промежутке [a,b]'); read(m);

x:=a; h:=(b-a)/m;

for i:=0 to m do

begin writeln (x:10:3, y:15:4);

y:=y+h*f(x,y); x:=x+h

end; readln;

end.

Блок-схема решения ДУ методом Эйлера	Результаты выполнения программы
	Введите значения концов отрезка [a,b] 0 1.57 Введите начальное значение y0=y(x0) Введите число значений функции на промежутке [a,b] 0.000 0.0000 0.157 0.1570 0.314 0.3121 0.471 0.4614 0.628 0.6013 0.785 0.7283 0.942 0.8394 1.099 0.9317 1.256 1.0031 1.413 1.0517 1.570 1.0764

Дата добавления: 2014-01-06