Методы Рунге-Кутта

Численные методы решения задачи Коши 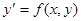, y(x₀)=y₀ на равномерной сетке { x₀=a, x₁, x₂, …, x_m=b } отрезка [ a, b ] с шагом 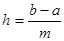являются методами Рунге-Кутта, если, начиная с данных y(x₀)=y₀ решение ведется по следующим рекуррентным формулам:

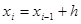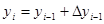; (i=1, 2, …, m) (7)

,

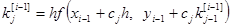
Метод называют методом Рунге-Кутта порядка P, если от имеет P -й порядок точности по шагу h на сетке.

Метод Эйлера можно назвать методом Рунге-Кутта первого порядка.

Метод Рунге-Кутта второго порядка называют методом Эйлера-Коши, если P=2, c₁=0, c₂=1, d₁=d₂=1/2

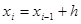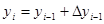; (i=1, 2, …, m) (8)

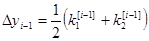
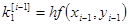
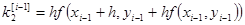
Для практической реализации погрешности решения можно применять правило Рунге, полагая P =2: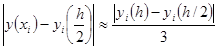

Программа решения дифференциального уравнения методом Эйлера-Коши:

program Eiler_Koshi;

var x,a,b,h,y,z:real;

m,i:integer;

function f(x,y: real): real;

begin f:=cos(x);

end;

begin writeln('Введите значения концов отрезка [a,b]');

readln(a,b);

writeln('Введите начальное значение y0=y(x0)');readln(y);

writeln('Введите число значений функции на промежутке [a,b]');

read(m);

x:=a; h:=(b-a)/m;

for i:=0 to m do

begin writeln (x:10:3, y:15:4);

z:=y+h*f(x,y);

y:=y+h*(f(x,y)+f(x+h,z))/2;

x:=x+h

end; readln;

end.

Введите значения концов отрезка [a,b]

0 1.57

Введите начальное значение y0=y(x0)

Введите число значений функции на промежутке [a,b]

0.000 0.0000

0.157 0.1560

0.314 0.3082

0.471 0.4528

0.628 0.5863

0.785 0.7054

0.942 0.8071

1.099 0.8889

1.256 0.9489

1.413 0.9855

1.570 0.9979

Классический метод Рунге-Кутта

Метод Рунге-Кутта четвертого порядка получаем при

P=4, c₁=0, c₂= c₃=1/2, c₄=1, d₁=d₄=1/6, d₂=d₃=1/3

Расчетные формулы имеют вид:

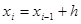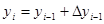; (i=1, 2, …, m) (9)

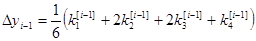
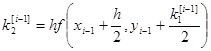
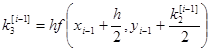
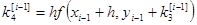
То есть берутся 4 направления и усредняются.

Для практической реализации погрешности решения можно применять правило Рунге, полагая P =4:

Программа решения дифференциального уравнения методом Рунге-Кутта:

program RungeKutta; {*** Mетод Рунге - Кутта ***}

var d,x,a,b,h,y,k1,k2,k3,k4:real;

m,i:integer;

function f(x,y: real): real;

begin f:=cos(x);

end;

BEGIN writeln('Введите значения концов отрезка [a,b]');

readln(a,b);

writeln('Введите начальное значение y0=y(x0)');readln(y);

writeln('Введите число значений функции на промежутке [a,b]');

read(m);

x:=a; h:=(b-a)/m;

for i:=0 to m do

begin writeln (x:10:3, y:15:4);

k1:=h*f(x,y);

k2:=h*f(x+h/2,y+k1/2);

k3:=h*f(x+h/2,y+k2/2);

k4:=h*f(x+h,y+k3);

d:=(k1+k2*2+k3*2+k4)/6; y:=y+d; x:=x+h

end; readln;

END.

Введите значения концов отрезка [a,b]

0 1.57

Введите начальное значение y0=y(x0)

Введите число значений функции на промежутке [a,b]

0.000 0.0000

0.157 0.1564

0.314 0.3089

0.471 0.4538

0.628 0.5875

0.785 0.7068

0.942 0.8087

1.099 0.8908

1.256 0.9509

1.413 0.9876

1.570 1.0000

Дата добавления: 2014-01-06