Закон распределения Больцмана

Распределение молекул по скоростям (Закон Максвелла)

Поскольку значение скоростей молекул может быть бесконеч­но большое, а само число молекул ограниченно, то находят не число молекул, обладающих той или иной скоростью, а число молекул или их часть, обладающих скоростями, лежащими в некотором интервале 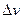вблизи заданной скорости. Например, число молекул, скорости которых лежат в пределах от 500 до 510 м/с ().

Относительное число молекул 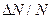, скорости которых лежат в интервале , зависит од скорости V и тем больше, чем больше и 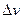, т.е.

(8.2)

функция называется функцией распределения. При 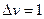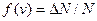, т.е. равна доле молекул, скорости которых заключены в единичном интервале скоростей. Так, как 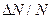имеет смысл вероятности, то - вероятность того, что молекула газа имеет скорость, заключенную в единичном интервале вблизи 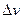. Можно графически представить зависимость от скорости . Число молекул , имеющих скорости , равны нулю.

Поэтому искомая зависимость, как следует из математики, должна иметь максимум при и асимптотически приближаться к оси абсцисс при (рис. 8.1). Аналитический вид ее для одинаковых молекул был рассчитан Максвеллом и. носит название закона распределения скоростей Максвелла:

(8.3)

Максимум этой функции при означает, что наибольшая доля всех молекул движется со скоростями, близкими к . Эту скорость поэтому называют наивероятной скоростью. Пользуясь кривой распределения, модно найти долю молекул 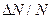, имеющих скорость в заданной интервале 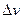.Она равна площади заштрихованной полосы. Вся же площадь под кривой дает полное число молекул я данном объёме. С повышением температуры скорости молекул возрастают, и кривая смещается в сторону больших скоростей (Рис. 8.2). Пользуясь (8.3) можно вычислить среднюю арифме­тическую и наивароятную ско­рость . Вычисления дают:

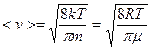(8.4); (8.5)

Для решения практических задач удобно закон Максвелла (8.3) записывать через относительную скорость . Из (8.5) и (8.3) можно получить:

(8.6)

В таком виде обычно пользуются законом Максвелла для решения задач, связанных с распределением молекул по скоростям. Экспериментальная проверка формулы распределения Максвелла впервые была проведена О. Штерном в 1920 г.

Рассмотрим теперь влияние внешнего силового поля, например, силы тяжести на поведение молекул идеального газа. Если бы отсутствовало тепловое движение, то все молекулы под дейст­вием силы тяжести скопились бы у поверхности Земли, и, наобо­рот, в отсутствие силы тяжести все молекулы разлетелись бы по всему пространству. Одновременное действие обоих процессов и приводит к установлению определенного распределения молекул по высоте, соответственно чему распределяется и давление газа. Рассмотрим вертикальный столб газа (Рис. 8.3). При изменении высоты на давление меняется на . На некоторой высоте оно равно давлению столба газа:

(8.7)

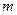где - плотность газа, - масса молекулы, 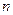- концентрация молекул. Из формулы (7.10). находим и 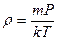. Под­ставив это в (8.7), получим:, откуда находим:

(8.8)

Так как ,, то вместо (8.8) получим:

(8.9)

Формулы (8.8) и (8.9), устанавливающие закон убывания давления с высотой, называют барометрической формулой.

Так как давление газа пропорционально числу молекул, то (8.8) и (8.9) выражают также и закон убывания концентраций молекул:

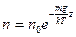(8.10)

Эта формула была использована Перроном (1909 г.) для опытней проверки барометрической формулы и числа Авогадро. В формуле (8.10) есть потенциальная энергия молекулы на высоте, то есть эта формула определяет число молекул (частиц) с энергией при нулевом уровне потенциальной энергии.

Если газ находится в другом силовом поле, так что его потенциальная энергия 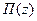, то число частиц с такой энергией определится формулой:

(8.11)

Эту формулу называют формулой Больцмана.

Дата добавления: 2014-01-06