Число столкновений и средняя длина свободного пробега молекул

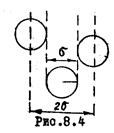
Имея большие скорости, молекулы газа в то же время перемещаются сравнительно медленно. Подтверждение тому, например, опыты по диффузии газов. Это объясняется большим числом столк­новений, которые испытывают молекулы газа между собой. Сред­ний путь, который проходит молекула между двумя столкновениями, называют средней длиной свободного пробега 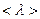. Для ее опре­деления вычислим вначале число столкновений данной молекулы о остальными за 1 с. Двигаясь, молекула вырезает в пространстве цилиндрический объем и сталкива­ется со всеми молекулами, центры которых лежат внутри цилиндра длиной 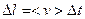и сечением. Если все остальные молекулы считать неподвижными, то за число столкновений будет ,где 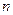- концентрация. Расчет с одновременным движением всех молекул дает уточнен­ную формулу:

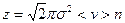(8.12)

Подсчет значения при комнатной температуре () и атмосферном давлении (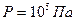) дает значение . Средняя длина свободного пробега определится так: , где 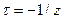- время свободного пробега, или

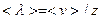(8.13)

В (8.12), (8.13) - так называемый эффективный диаметр молекулы - диаметр площади, в которую должна попасть летящая молекула, чтобы испытать столкновение.

Лекция 11	Первое начало термодинамики. Работа газа при изменении объёма. Теплота и теплоёмкость.
	Изопроцессы и адиабатический процесс. Работа и теплоёмкость газа в этих процессах. Графическое изображение термодинамических процессов.

Дата добавления: 2014-01-06