Энтропия. Рассмотрим, как математически формулируется второе нача­ло термодинамики

Рассмотрим, как математически формулируется второе нача­ло термодинамики.

Для обратимого цикла Карно:

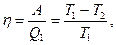откуда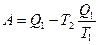

Эта формула определяет максимальную работу, получаемую при превращении тепла в работу. Часть тепла, равная 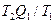, при этом не может быть превращена в работу, она передается ок­ружающим телам. Отношение 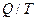как раз и характеризует ту часть тепла, которую нельзя превратить в работу. Это отношение явля­ется мерой неиспользованного тепла. Р. Э. Клаузис назвал эту ве­личину энтропией 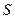(от греч. превращение).

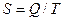(10.7)

Энтропия является как и внутренняя энергия 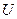функцией состояния и может быть выражена через параметры состояния системы :

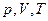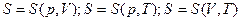
Она имеет размерность теплоемкости. В термодинамике её определяют через дифференциальное соотношение:

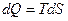(10.8)

Из (10.5) следует, что для обратимого цикла Карно 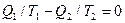или, т.к. 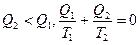(10.9)

Это соотношение справедливо для любого обратимого цикла 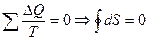или .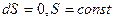

Отсюда следует, что для любых обратимых циклов энтропия остается постоянной.

Если цикл необратимый, то 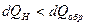и для такого цикла 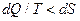. Если система теплоизолирована (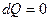), то для нее 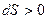, т.е. в ней возможны процессы, для которых энтропия возрастает.

С помощью энтропии математически формулируется второе начало термодинамики.

В изолированных системах возможны лишь процессы, при ко­торых энтропия возрастает: .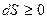

Итак, второе начало термодинамики связано с необратимостью реальных процессов, что, в свою очередь, обусловлено мо­лекулярной природой тепловых процессов, хаотичным движением молекул.

Из опыта известно, что в системе, состоящей из большого числа хаотически движущихся молекул, могут возникнуть самопроизвольные процессы, приводящие систему к равновесному состоянию (выравнивание температур, концентраций и т.д.). Обрат­ные из процессы практически не наблюдаются, т.е. они малове­роятны. Таким образом, необратимость тепловых процессов имеет вероятностный характер.

В равновесном состоянии частицы равномерно распределены по всему объему тела, поэтому вероятность такого состояния наибольшая, следовательно, процессы идут в сторону увеличения вероятности состояния. С другой стороны, энтропия процесса возрастает, т.е. энтропия системы связана с вероятностью состояния, в этом заключается статистический смысл энтропии и второго начала термодинамики.

Количественной характеристикой теплового состояния тела может служить число микроскопических способов, которым это состояние может быть осуществлено. Это число называют термоди­намической вероятностью или статистическим весом 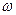. Как сле­дует из вышесказанного, должна существовать функциональная зависимость между 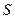и .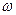

Такая зависимость была установлена Л. Больцманом, который показал, что:

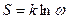(10.10)

где 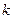- постоянная Больцмана.

Лекция 16	Реальные газы. Сила и потенциальная энергия межмолекулярного взаимодействия.
	Уравнение Ван-дер-Ваальса для реального газа. Изотермы уравнения. Метастабильные состояния.

Дата добавления: 2014-01-06