Критическое состояние вещества

Уравнение состояния реального газа (уравнение Ван-дер-Ваальса)

Для 1 моля идеального газа уравнение состояния имеет вид , где - объем, предоставленный молекулам газа. Для реальных газов некоторая его часть занята самими моле­кулами. Поэтому объем надо заменить разностью .

Учтем теперь взаимодействие молекул. Силы притяжения, действующие между молекулами, приводят, к уменьшению давления газа на стенки сосуда на некоторую величину , так что:

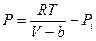или (11.1)

где - дополнительное давление, обусловленное силами притя­жения. Его называют также внутренним или молекулярным давлени­ем. Это давление пропорционально концентрации молекул и силе, действующей на данную молекулу со стороны остальных, которая в свою очередь, также пропорциональна концентрации молекул. Таким образом, или , где 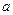- пос­тоянная, характеризующая силы молекулярного притяжения и зави­сящая от природы газа. Таким образом, получаем для 1 моля уравнение:

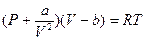(11.2)

Это уравнение состояния реального газа или уравнение Ван-дер-Ваальса; 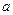и - константы, определяемые экспериментально. Исследуем уравнений (11.2), для чего перепишем его в виде:

(11.3)

С его помощью можно построить теоретические изотермы ре­ального газа - зависимость от при заданных значениях .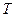

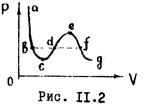
Уравнение (11.3) - уравнение третьей степени относитель­но . Поэтому оно может иметь либо три действительных корня, либо один. Одна из таких изотерм изображена на рис. 11.2. На участках ,, т.е. с увеличением давления объем уменьшается, на участке же , что соответству­ет неестественному состоянию вещества, когда сжатие приводит к увеличению объема. Поэтому на опыта изотерма пожег быть лишь вида (Рис. 11.3). Такая изотерма действительно была получена Т. Эндрьюсом с углекислотой. Наличии горизонтального участка связано с тем, что при изменении объема вещество не может все время оставаться в однофазном состо­янии. В некоторый момент про­исходит скачкообразной измене­ние состояния вещества и его распадение на две фазы: жидкую () и газообразную (). Горизонтальный участок () соответ­ствует двухфазному состоянию вещества - переходу газа в жид­кость при заданных температуре и давлении. Эта область насы­щенного пара.

Лекция 17	Изотермы реальных газов. Сравнение уравнения Ван-дер-Ваальса с экспериментальными данными.
	Фазовые переходы 1-го и 2-го рода. Критическое состояние.

Экспериментальные изотермы при различных температурах изображены на рис. 11.4. Как видно, с ростом температуры го­ризонтальные участки становят­ся все короче. При некоторой температуре прямолинейный от­резок исчезает и на изотерме остается лишь точка перегиба . Это означает, что исчезает переход из газообразного сос­тояния в жидкое и наоборот, исчезает разница между жидким и газообразным.

Это состояние называется критическим состоянием, а температура, при которой оно наступает - критической температурой . Понятие критической температуры было введено Д. И. Менде­леевым.

При температурах выше критической вещество может сущест­вовать только в газообразном состоянии и никакими способами не может быть переведено в жидкое.

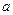Критической температуре соответствует критическое дав­ление и критический объем . Совокупность этих величин и характеризует критическое состояние. Так, например, для воды ; для углекислого газа ; для водорода . Критические параметры связаны с поправками и уравнения Ван-дер-Ваальса.

Уравнение (11.3), как говорилось, может иметь либо три действительных корня - ниже , либо один при . Поэтому (11.3) можно в этом случае записать в виде:

Сравнивая коэффициенты этого уравнения с (11.3) при одинаковых степенях, где , получаем:

, откуда

.

Лекция 18	Внутренняя энергия реального газа. Эффект Джоуля – Томсона и его физическая сущность.
	Сжижение газов и получение низких температур.

Дата добавления: 2014-01-06