Теорема Гаусса

Основное соотношение между источником и полем можно выразить с помощью потока вектора напряженности через замкнутую поверхность, охватывающую данный заряд. Этот поток является мерой полного воздействия заряда на пространство, окружающее его. Вычислим для простоты поток вектора 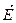поля точечного заряда 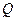через сферическую поверхность, центр которой совпадает с положением заряда.

По формуле (13.12) имеем 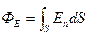. Т.к. для шаровой поверхности 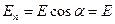, то 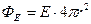. Используя формулу напряженности (13.7) и (13.3), находим:

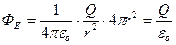(13.13)

Этот результат обобщается на произвольную замкнутую поверхность, охватывающую заряд 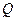: поток вектора напряженности электрического поля через любую замкнутую поверхность, охватывающую заряд 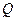, не зависит от формы поверхности и равен 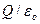. Для системы зарядов в силу принципа суперпозиции (13.10):

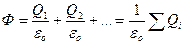(13.14)

Итак, полный поток вектора напряженности электрического поля, выходящий из замкнутой поверхности, пропорционален алгебраической сумме зарядов, охватываемых этой поверхностью (теорема Гаусса).

Если внутри поверхности зарядов нет, то из теоремы следует, что поток силовых линий через нее равен нулю.

Теорема Гаусса позволяет вычислять напряженности полей, создаваемые зараженными телами простой формы.

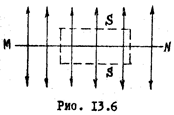
Вычислим для примера напряженность поля бесконечно заряженной плоскости о поверхностной плотностью заряда . Из соображений симметрии ясно, что вектор напряженности поля 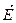должен быть направлен перпендикулярно плоскости (Рис.13.6).

Пусть плоскость пересечена поверхностью прямого параллелепипеда с площадью основания 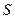. Напряженность поля будет перпендикулярна к основаниям и параллельна остальным граням. Поток через основания в силу теоремы Гаусса равен 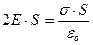, откуда напряженность поля заряженной плоскости равна:

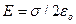(13.15)

Для пространства между двумя разноименно заряженными плоскостями:

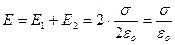(13.16)

Лекция 21	Работа поля по перемещению заряда. Потенциал электрического поля, его связь с напряжённостью. Энергия системы зарядов.
	Проводники в электростатическом поле. Распределение зарядов и поля в проводнике.

Дата добавления: 2014-01-06