Модель у. Шарпа

Уравнение модели

Ожидаемую доходность актива можно определить не только с помощью уравнения SML, но также на основе так называемых индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависит от ряда показателей, характеризующих состояние рынка, или индексов.

Простая индексная модель предложена У. Шарпом в середине 60-х годов. Ее часто называют рыночной моделью. В модели Шарпа представлена зависимость между ожидаемой доходностью актива и ожидаемой доходностью рынка. Она предполагается линейной. Уравнение модели имеет следующий вид:

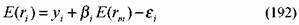
где: E(ri) — ожидаемая доходность актива;

Yi — доходность актива в отсутствии воздействия на него рыночных факторов;

βi — коэффициент бета актива;

Е(rm) — ожидаемая доходность рыночного портфеля;

εi — независимая случайная переменная (ошибка): она показывает специфический риск актива, который нельзя объяснить действием рыночных сил. Значение ее средней равно нулю. Она имеет постоянную дисперсию; ковариацию с доходностью рынка равную нулю; ковариацию с нерыночным компонентом доходности других активов равную нулю.

Уравнение (192) является уравнением регрессии. Если его применить к широко диверсифицированному портфелю, то значения случайных переменных (εi) в силу того, что они изменяются как в положительном, так и отрицательном направлении, гасят друг друга, и величина случайной переменной для портфеля в целом стремится к нулю. Поэтому для широко диверсифицированного портфеля специфическим риском можно пренебречь. Тогда модель Шарпа принимает следующий вид:

портфеля;

βp — бета портфеля;

ур — доходность портфеля в отсутствии воздействия на него рыночных факторов.

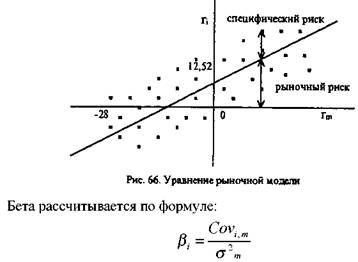
Графически модель Шарпа представлена на рис. 66 и 67. Она показывает зависимость между доходностью рынка (rт) и доходностью актива (ri) и представляет собой прямую линию. Ее называют линией характеристики. Независимой переменной выступает доходность рынка. Наклон линии характеристики определяется коэффициентом бета, а пересечение с осью ординат — значением показателя уi.

YI можно определить из формулы (193), взяв средние значения доходности рынка и актива за предыдущие периоды времени. 1

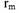— средняя доходность рынка.

Пример.

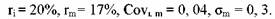Определить уравнение рыночной модели.

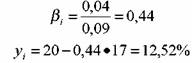модели имеет вид:

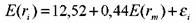представлено на рис. 66. Точками показаны конкретные значения доходности i-го актива и рынка для различных моментов времени в прошлом.

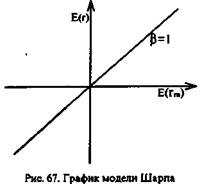
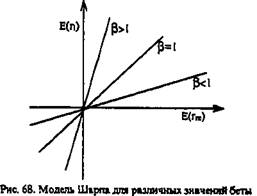
На рис. 66 и рис. 67 представлен случай, когда бета положительна, и поэтому график рыночной модели направлен вправо вверх, т. е. при увеличении доходности рынка доходность актива будет повышаться, при понижении — падать. При отрицательном значении беты график направлен вправо вниз, что говорит о противоположном движении доходности рынка и актива. Более крутой наклон графика говорит о высоком значении беты и большем риске актива, менее крутой наклон — о меньшем значении беты и меньшем риске (см. рис. 68). При β = 1 доходность актива соответствует доходности рынка, за исключением случайной переменной, характеризующей специфический риск.

Если построить график модели для самого рыночного портфеля относительно рыночного портфеля, то значение у для него равно нулю, а беты +1. Графически данная модель представлена на рис. 67.

15. 3. 2. Коэффициент детерминации

Рыночную модель можно использовать для того, чтобы разделить весь риск актива на дивесифицируемый и недиверсифицируемый, Графически специфический и рыночный риски представлены на рис. 68. Согласно модели Шарпа дисперсия актива равна:

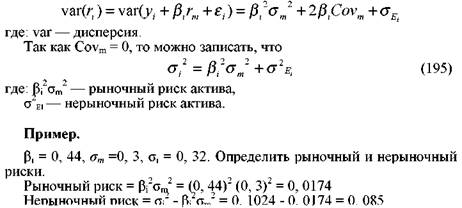
Для вычисления доли дисперсии актива, которая определяется рынком, используют коэффициент детерминации (R2). Он представляет собой отношение объясняемой рынком дисперсии актива к его общей дисперсии.

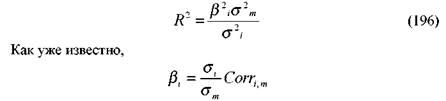
Подставив данное значение в формулу (196), получим результат, который говорит о том, что коэффициент детерминации — это квадрат коэффициента корреляции.

R2 = (Corri,m)2 (197)

R2 = (Corri,m)2 (197)

В последнем примере R-квадрат равен 0, 1699. Это означает, что изменение доходности рассматриваемого актива можно на 16, 99% объяснить изменением доходности рынка, а на 83, 01% — другими факторами. Чем ближе значение R-квадрат к единице, тем в большей степени движение рынка определяет изменение доходности актива. Обычное значение R-квадрат в западной экономике составляет порядка 0, 3, т. е. 30% изменения его доходности определяется рынком. R-квадрат для широко диверсифицированного портфеля может составлять 0, 9 и большую величину.

Дата добавления: 2014-01-06